Calculus笔记-16.7-曲面积分

Calculus笔记-16.7-曲面积分

曲面积分和曲面面积的关系与直线积分和弧长的关系是一致的。设 $f$ 是一个三元函数，其定义域是一个曲面 $S$ 。我们定义 $f$ 的曲面积分是满足在 $f(x, y, z) = 1$ 时其值等于 $S$ 的面积的积分。我们首先从参数曲面开始，再讨论 $S$ 是二元函数的图像的特例。

数量场的曲面积分

对参数曲面的积分

定义

$$\text{设 $S$ 由向量方程}\\ \mathbf r(u, v) = x(u, v)\mathbf i + y(u, v)\mathbf j + z(u, v)\mathbf k \qquad(u, v)\in D\\ \text{所确定，则 $f$ 对曲面 $S$ 的曲面积分为}\\ \iint\limits_Sf(x, y, z)dS = \lim_{m, n\to\infty} \sum_{i = 1}^m\sum_{j = 1}^nf(P_{ij})\Delta S_{ij} = \iint\limits_Df(\mathbf r(u, v))|\mathbf r_u\times\mathbf r_v|dA\\ \text{其中 $\mathbf r_u,\ \mathbf r_v\ne\mathbf 0$ 且 } \text{ $\mathbf r_u,\ \mathbf r_v$ 不平行} \tag{7.1}\label{数量场曲面积分的定义}$$

可以计算出， $\iint\limits_S1dS = \iint\limits_D|\mathbf r_u\times\mathbf r_v|dA = A(S)$ ，因此这个定义满足我们的要求。

曲面积分的物理意义

形状为 $S$ ，在 $(x, y, z)$ 点密度为 $\rho(x, y, z)$ 的薄片，其质量(mass)为

$$m = \iint\limits_S\rho(x, y, z)dS$$

质心坐标为 $(\bar x, \bar y, \bar z)$ ，其中

$$\bar x = \iint\limits_Sx\rho(x, y, z)dS\qquad \bar y = \iint\limits_Sy\rho(x, y, z)dS\qquad \bar z = \iint\limits_Sz\rho(x, y, z)dS$$

转动惯量也可以用类似的定义写出来。

对函数图像的积分

任何由方程 $z = g(x, y)$ 所表示的曲面 $S$ 都可被看作由参数方程

$$x = x\qquad y = y\qquad z = g(x, y)$$

所表示的参数曲面，因此我们有：

$$\mathbf r_x = \mathbf i + \left(\frac{\partial g}{\partial x}\right)\mathbf k \qquad \mathbf r_y = \mathbf j + \left(\frac{\partial g}{\partial y}\right)\mathbf k$$

因此

$$\mathbf r_x\times\mathbf r_y = -\frac{\partial g}{\partial x}\mathbf i -\frac{\partial g}{\partial y}\mathbf j +\mathbf k \tag{7.2}\label{函数图像的法线}$$

而

$$|\mathbf r_x\times\mathbf r_y| = \sqrt{ \left( \frac{\partial z}{\partial x} \right)^2 + \left( \frac{\partial z}{\partial y} \right)^2 + 1 }$$

因此式 $\eqref{数量场曲面积分的定义}$ 变为

$$\iint\limits_Sf(x, y, z)dS = \iint\limits_Df(x, y, g(x, y)) \sqrt{ \left( \frac{\partial z}{\partial x} \right)^2 + \left( \frac{\partial z}{\partial y} \right)^2 + 1 }dA \tag{7.3}\label{对函数图像的曲面积分}$$

式 $\eqref{对函数图像的曲面积分}$ 表示对函数在定义域 $D$ 内图像的曲面积分。

---

当 $z$ 不是因变量而是自变量时，式 $\eqref{对函数图像的曲面积分}$ 同样可以化为相应的形式，比如当 $S$ 满足方程为 $y = h(x, z)$ ，而 $D$ 是 $S$ 在 $xz$ 平面上的投影时，

$$\iint\limits_Sf(x, y, z)dS = \iint\limits_Df(x, h(x, z), z) \sqrt{ \left( \frac{\partial y}{\partial x} \right)^2 + \left( \frac{\partial y}{\partial z} \right)^2 + 1 }dA.$$

向量场的曲面积分

有向曲面

对向量场计算其曲面积分时会遇到朝向的问题。因此我们需要事先规定曲面的正方向。

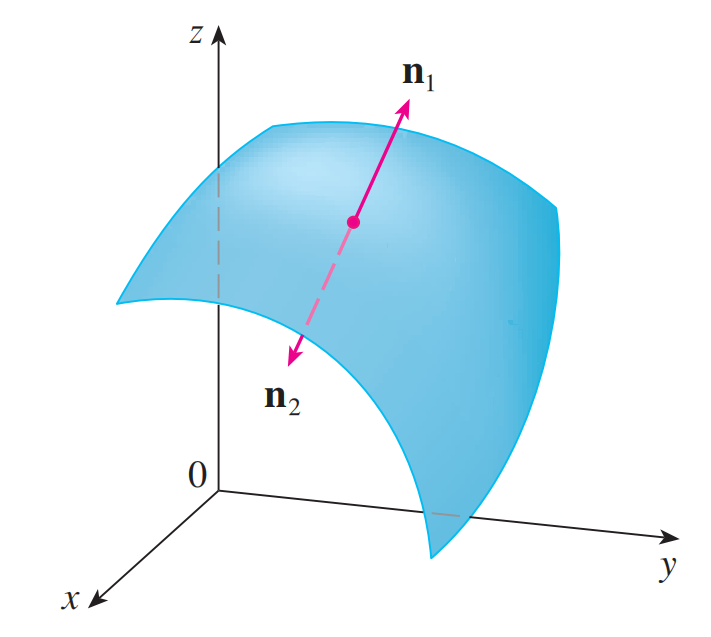
如上图，对任意可定向（有两个面）的曲面，其在 $(x, y, z)$ 点会有两个方向相反的法向量 $\mathbf n_1$ 和 $\mathbf n_2 = -\mathbf n_1$ 。

如果可以在任意的点 $(x, y, z)$ 选取 $\mathbf n$ ，使得 $\mathbf n$ 在 $S$ 上连续变化，则 $S$ 被称为有向曲面(oriented surface)，而这时对于 $\mathbf n$ 的选取被称为一个朝向(orientation)。任意可定向的曲面都会有两种朝向。

对曲面 $z = g(x, y)$ ，我们用式 $\eqref{函数图像的法线}$ 来表示其自然朝向(natural orientation)，其单位法向量为

$$\mathbf n = \frac { -\frac{\partial g}{\partial x}\mathbf i -\frac{\partial g}{\partial y}\mathbf j +\mathbf k } { \sqrt{ \left( \frac{\partial z}{\partial x} \right)^2 + \left( \frac{\partial z}{\partial y} \right)^2 + 1 } } \tag{7.4}\label{函数图像单位法向量}$$

因为 $\mathbf k$ 分量是正数，式 $\eqref{函数图像单位法向量}$ 给出了曲面的上(upward)朝向

---

如果 $S$ 是一个由参数方程 $\mathbf r(u, v)$ 给出的光滑有向曲面，则它的朝向由单位法向量

$$\mathbf n = \frac {\mathbf r_u\times\mathbf r_v} {|\mathbf r_u\times\mathbf r_v|} \tag{7.5}\label{参数曲面单位法向量}$$

给出，而与其相反的朝向则由 $-\mathbf n$ 给出。

---

对于闭合曲面(closed surface)即其本身为空间区域 $E$ 的边界的曲面，通常将其正向(positive orientation)设为法向量指向 $E$ 的外侧的朝向。

曲面积分的引入

设 $S$ 是单位法向量为 $\mathbf n$ 的有向曲面，而密度为 $\rho(x, y, z)$ ，速度场为 $\mathbf v(x, y, z)$ 的流体正在流经 $S$ 。则其单位面积的流速为 $\rho\mathbf v$ 。

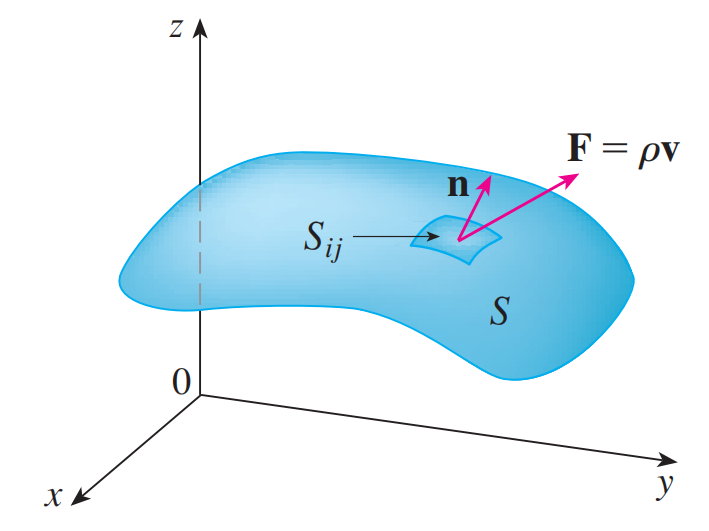
如图，若将 $S$ 分成小块 $S_{ij}$ ，则 $S_{ij}$ 近似于平面。因为 $\rho\mathbf v$ 沿单位法向量 $\mathbf n$ 的分量为 $\rho\mathbf v\cdot\mathbf n$ ，我们可以将单位时间沿 $\mathbf n$ 流经 $S_{ij}$ 的流体质量近似为

$$(\rho\mathbf v\cdot\mathbf n)A(S_{ij})$$

，其中 $\rho,\ \mathbf v$ 和 $\mathbf n$ 的值在 $S_{ij}$ 内的某一点取得。对这些量求和并取极限，我们可以得到函数 $\rho\mathbf v\cdot\mathbf n$ 对 $S$ 的曲面积分：

$$\iint\limits_S\rho\mathbf v\cdot\mathbf ndS = \iint\limits_S\rho(x, y, z)\mathbf v(x, y, z) \cdot\mathbf n(x, y, z)dS \tag{7.6}\label{流速的曲面积分}$$

其物理意义为经过 $S$ 的液体流速。

---

若令 $\mathbf F = \rho\mathbf v$ ，则 $\mathbf F$ 也是在 $\mathbb R^3$ 上的向量场，而式 $\eqref{流速的曲面积分}$ 变为

$$\iint\limits_S\mathbf F\cdot\mathbf ndS$$

这样形式的曲面积分在物理中经常出现，即使在 $\mathbf F$ 不为 $\rho\mathbf v$ 时。而这种积分被称为 $\mathbf F$ 对 $S$ 的曲面积分(surface integral)或通量积分(flux integral)。

向量场曲面积分的定义

$$\text{若 $\mathbf F$ 是在有向曲面 $S$ 上有定义的连续向量场，其单位法向量为 $\mathbf n$ ，则 $\mathbf F$ 对 $S$ 的曲面积分为}\\ \iint\limits_S\mathbf F\cdot d\mathbf S = \iint\limits_S\mathbf F\cdot\mathbf ndS\\ \text{这个积分也被称为 $F$ 对 $S$ 的通量.} \tag{7.7}\label{向量场曲面积分的定义}$$

定义 $\eqref{向量场曲面积分的定义}$ 的意思是，向量场对 $S$ 的曲面积分等于其法向分量对 $S$ 的积分。这和定义 $\eqref{数量场曲面积分的定义}$ 是一致的。

对参数曲面的积分

若 $S$ 由位矢函数 $\mathbf r(u, v)$ 给出，则 $\mathbf n$ 由式 $\eqref{参数曲面单位法向量}$ 给出。由定义 $\eqref{向量场曲面积分的定义}$ 和等式 $\eqref{数量场曲面积分的定义}$ ，我们有：

$$\begin{align} \iint\limits_S\mathbf F\cdot d\mathbf S &= \iint\limits_S\mathbf F\cdot \frac{\mathbf r_u\times\mathbf r_v} {|\mathbf r_u\times\mathbf r_v|} dS \\&= \iint\limits_S \left[ \mathbf F(\mathbf r(u, v))\cdot \frac{\mathbf r_u\times\mathbf r_v} {|\mathbf r_u\times\mathbf r_v|} \right] |\mathbf r_u\times\mathbf r_v| dA \end{align}$$

其中 $D$ 为参数定义域。

则有：

$$\iint\limits_S\mathbf F\cdot d\mathbf S = \iint\limits_S\mathbf F\cdot(\mathbf r_u\times\mathbf r_v)dA. \tag{7.8}\label{向量场对参数曲面的积分}$$

对函数图像的积分

当 $S$ 由图像 $z = g(x, y)$ 给出时，我们将 $x$ 和 $y$ 当作参数，结合方程 $\eqref{函数图像单位法向量}$ 可以写出

$$\mathbf F\cdot(\mathbf r_x\times\mathbf r_y) = (P\mathbf i + Q\mathbf j + R\mathbf k)\cdot \left( -\frac{\partial g}{\partial x}\mathbf i -\frac{\partial g}{\partial y}\mathbf j +\mathbf k \right)$$

则式 $\eqref{向量场对参数曲面的积分}$ 变为

$$\iint\limits_S\mathbf F\cdot d\mathbf S = \iint\limits_D \left( -\frac{\partial g}{\partial x}P -\frac{\partial g}{\partial y}Q +\mathbf R \right)dA \tag{7.9}\label{向量场对函数图像的积分}$$

式 $\eqref{向量场对函数图像的积分}$ 假设了 $S$ 是向上的。对于向下的曲面，我们将其乘以 $-1$ 。当 $S$ 由 $y = h(x, z)$ 或 $x = k(y, z)$ 给出时，我们也可以写出类似的公式。

高斯公式

除了引入中的流体，向量场的曲面积分也在其他物理领域有着广泛应用。

比如说，若 $\mathbf E$ 是一个电场，则曲面积分

$$\iint\limits_S\mathbf E\cdot d\mathbf S$$

表示 $\mathbf E$ 穿过曲面 $S$ 的电通量(electric flux)。高斯公式指出，由闭合曲面 $S$ 所包围的电荷量等于

$$Q = \varepsilon_0\iint\limits_S\mathbf E\cdot d\mathbf S \tag{7.10}\label{高斯公式}$$

其中 $\varepsilon_0$ 是真空介电系数。