Calculus笔记-16.6-参数曲面及面积

Calculus笔记-16.6-参数曲面及面积

参数曲面

正如参数曲线一样，参数曲面是一个向量值函数，但其自变量有两个。

设

$$\mathbf r(u, v) = x(u, v)\mathbf i + y(u, v)\mathbf j + z(u, v)\mathbf k \tag{6.1}\label{曲面参数方程}$$

为定义在 $uv$ 平面内的区域 $D$ 上的向量值函数，而 $\mathbf r$ 的三个分量函数 $x,\ y,\ z$ 都为定义域为 $D$ ，自变量为 $u$ 和 $v$ 的二元函数。所有在 $\mathbb R^3$ 内，在 $(u, v)$ 遍历整个 $D$ 时满足

$$x = x(u, v)\qquad y = y(u, v)\qquad z = z(u, v) \tag{6.2}\label{曲面分量方程}$$

的点集 $(x, y, z)$ 被称为参数曲面(parametric surface) $S$ ，而方程 $\eqref{曲面分量方程}$ 被称作 $S$ 的参数方程(parametric equations)。任何 $u$ 和 $v$ 的取值都对应 $S$ 上的一个点，而所有 $u$ 和 $v$ 的取值则对应整个曲面 $S$ 。

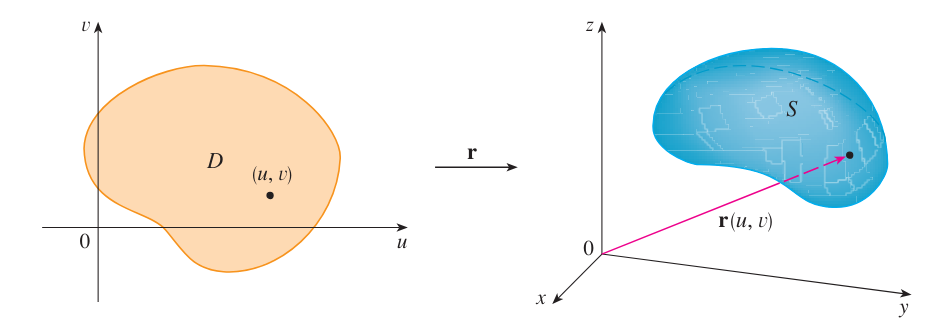
因此曲面 $S$ 被遍历整个 $D$ 时 $(u, v)$ 所对应的位矢 $\mathbf r(u, v)$ 的箭头终端所指示出来（如上图）。这反映出曲面的参数方程是一个从 $(u, v)$ 到 $(x, y, z)$ 的映射。

网格线(grid curves)

给定曲面 $S$ 的参数方程 $\mathbf r(u, v)$ ，若令 $u = u_0$ ，则 $\mathbf r(u_0, v)$ 成为关于 $v$ 的一元向量值函数；令 $v = v_0$ ，则 $\mathbf r(u, v_0)$ 成为关于 $u$ 的一元向量值函数。

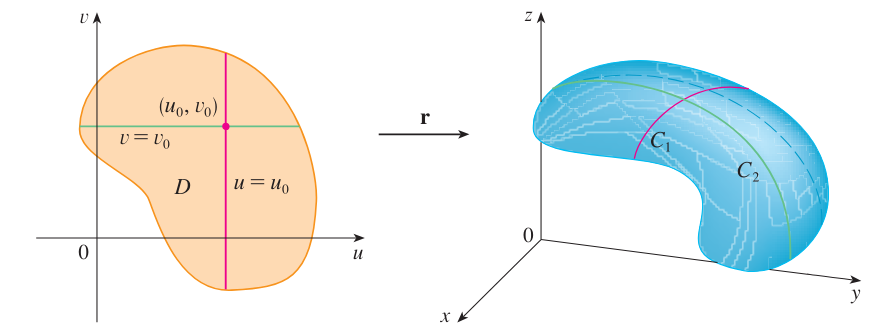
如上图，这两个函数所分别确定的两条曲线被称为网格线。

旋转曲面

我们可以用参数方程来表示旋转曲面。

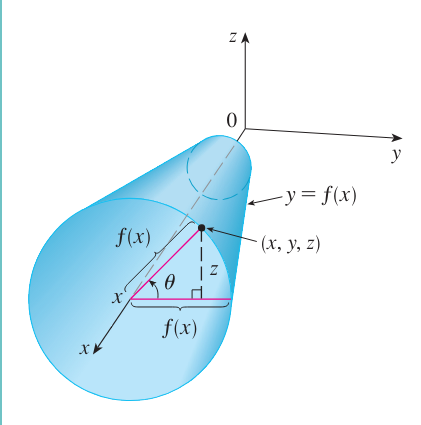
比如，想要得到将曲线 $y = f(x),\ a\le x\le b,\text{ 其中 } f(x)\ge 0$ 绕 $x$ 轴旋转所得到的曲面，则令 $\theta$ 为上图中的旋转角，若 $(x, y, z)$ 是 $S$ 上的点，则

$$x = x\qquad y = f(x)\cos\theta\qquad z = f(x)\sin\theta \tag{6.3}\label{旋转曲面参数方程}$$

则我们将 $x$ 和 $\theta$ 看作 $\eqref{旋转曲面参数方程}$ 的参数，其定义域为 $a\le x\le b,\ 0\le\theta\le 2\pi$ 。

绕其他轴旋转而得的旋转曲面也同理。

切平面(Tangent Planes)

为寻找由向量值函数

$$\mathbf r(u, v) = x(u, v)\mathbf i + y(u, v)\mathbf j + z(u, v)\mathbf k$$

所确定的参数曲面 $S$ 在 $P_0$ （其位矢为 $\mathbf r(u_0, v_0)$ ）的切平面，我们可以分别设 $u = u_0$ ， $v = v_0$ 而分别得到 $S$ 在 $P_0$ 的网格线，其切向量分别为

$$\mathbf r_v = \frac{\partial x}{\partial v}(u_0, v_0)\mathbf i + \frac{\partial y}{\partial v}(u_0, v_0)\mathbf j + \frac{\partial z}{\partial v}(u_0, v_0)\mathbf k \tag{6.4}\label{切向量1}$$ $$\mathbf r_u = \frac{\partial x}{\partial u}(u_0, v_0)\mathbf i + \frac{\partial y}{\partial u}(u_0, v_0)\mathbf j + \frac{\partial z}{\partial u}(u_0, v_0)\mathbf k \tag{6.5}\label{切向量2}$$

若 $\mathbf r_u\times\mathbf r_v\ne\mathbf 0$ ，则我们称 $S$ 为光滑(smooth)曲面。对于光滑曲面，其切平面为包含切向量 $\mathbf r_u$ 和 $\mathbf r_v$ ，且以 $\mathbf r_u\times\mathbf r_v$ 为法向量的平面。

曲面面积

曲面面积的推导已在 $15.5$ 节中进行过，在此不再赘述。现给出定义：

定义

$$\text{若光滑参数曲面 $S$ 由方程}\\ \mathbf r(u, v) = x(u, v)\mathbf i + y(u, v)\mathbf j + z(u, v)\mathbf k\qquad(u, v)\in D\\ \text{给出，且 $S$ 在 $(u, v)$ 在整个参数定义域 $D$ 内变化时只被覆盖过一次，}\\ \text{则 $S$ 的表面积为}\\ A(S) = \iint\limits_D|\mathbf r_u\times\mathbf r_v|dA\\ \text{其中} \qquad\mathbf r_u = \frac{\partial x}{\partial u}\mathbf i + \frac{\partial y}{\partial u}\mathbf j + \frac{\partial z}{\partial u}\mathbf k\qquad \mathbf r_v = \frac{\partial x}{\partial v}\mathbf i + \frac{\partial y}{\partial v}\mathbf j + \frac{\partial z}{\partial v}\mathbf k. \tag{6.6}\label{曲面面积的定义}$$

函数图像的面积

令方程 $z = f(x, y)$ ，其中 $(x, y)$ 在 $D$ 内而 $f$ 有连续偏导数，我们将 $(x, y)$ 看作参数。其参数方程为

$$x = x\qquad y = y\qquad z = f(x, y)$$

则

$$\mathbf r_x = \mathbf i + f_x(x, y)\mathbf k$$ $$\mathbf r_y = \mathbf j + f_y(x, y)\mathbf k$$

则

$$\mathbf r_x\times\mathbf r_x = \begin{vmatrix} \mathbf i & \mathbf j & \mathbf k\\ 1 & 0 & f_x\\ 0 & 1 & f_y \end{vmatrix} = -f_x\mathbf i - f_y\mathbf j + \mathbf k$$

因此有

$$|\mathbf r_x\times\mathbf r_x| = \sqrt{f_x^2 + f_y^2 + 1} = \sqrt{1 + f_x^2 + f_y^2}$$

则

$$A(S) = \iint\limits_D\sqrt{1 + f_x^2 + f_y^2}dA. \tag{6.7}\label{函数图像的面积}$$