Calculus笔记-16.4-格林公式

Calculus笔记-16.4-格林公式

我们约定给定区域的正向绕序为沿边界的逆时针方向，因此对于由曲线 $C$ 围成的简单连通区域 $D$ ，若 $C$ 由参数方程 $\mathbf r(t),\ a\le t\le b$ 确定，则其 $D$ 总在边界 $C$ 的左边：

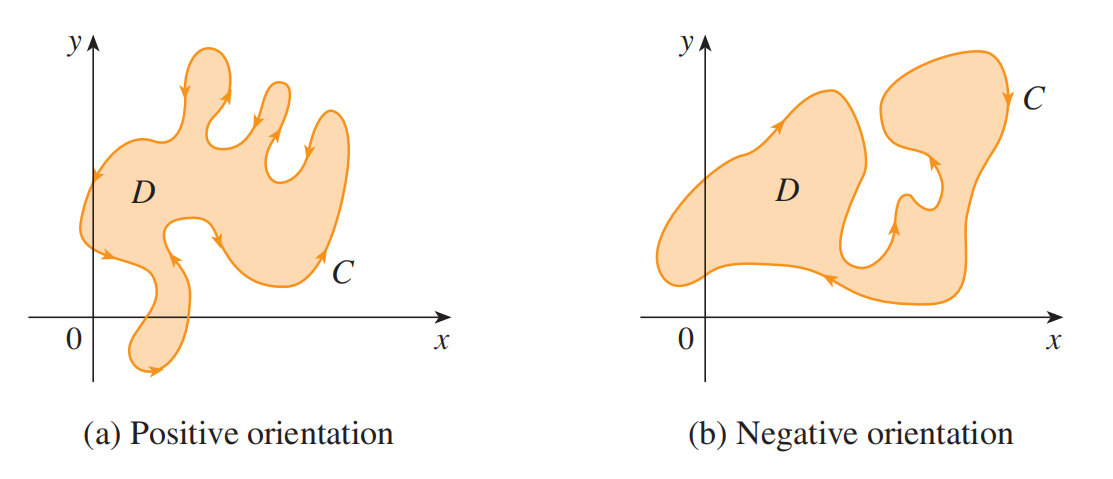
则我们有格林公式：

格林公式(Green’s Theorem)

令 $C$ 为一条正向绕序且（分段）光滑的简单闭合曲线，而 $D$ 为 $C$ 所围成的简单连通区域，且 $P$ 和 $Q$ 在包含 $D$ 的开简单连通区域内都有一阶连续偏导数，则有

$$\int_CPdx + Qdy = \iint\limits_D\left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)dA \tag{4.1}\label{格林公式1}$$

• 符号 $$\oint_C Pdx + Qdy$$ 被用来表示正向绕序、分段光滑的简单闭合曲线的直线积分。另一种表示 $D$ 的正向曲线边界的方法是 $\partial D$ ，则格林公式可被写为 $$\iint\limits_D\left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)dA = \int_{\partial D}Pdx + Qdy \tag{4.2}\label{格林公式2}$$

格林公式可被看为二重积分的微积分基本定理，它揭示了闭合曲线的直线积分和其所围成的平面的二重积分之间的关系。

格林公式的扩展

• 格林公式除了可以用在单个简单区域中，也可以被扩展到有限个简单区域的并中：

  

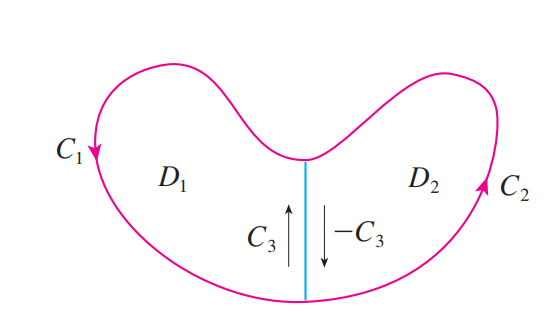
  如图，设 $D = D_1\cup D_2$ ， $D_1$ 和 $D_2$ 分别为有向曲线 $C_1,\ C_3$ 和 $C_2,\ -C_3$ 所围成的简单连通区域，则

  $$\int_{C_1\cup C_3}Pdx + Qdy = \iint\limits_{D_1}\left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)dA$$ $$\int_{C_2\cup -C_3}Pdx + Qdy = \iint\limits_{D_2}\left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)dA$$

  将两式相加，我们得到：

  $$\int_{C_1\cup C_2}Pdx + Qdy = \iint\limits_D\left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)dA$$

  因此，我们可以将格林公式扩展到任意有限个不互相包含的简单连通区域中。

• 格林公式也可以被扩展到非简单连通区域中：

  

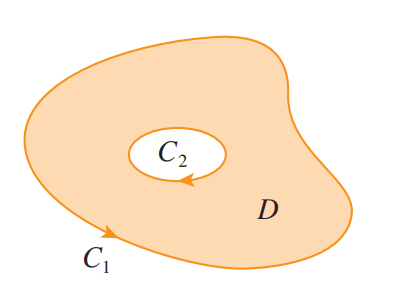
  如图，区域 $D$ 由两简单闭合曲线 $C_1$ 和 $C_2$ 围成。若我们规定曲线 $C_2$ 的正方向为顺时针方向，则 $D$ 同时位于两个曲线的左侧。

  

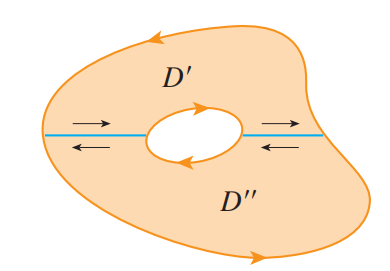
  则我们可以将 $D$ 分为两个区域 $D’$ 和 $D’’$ ，并分别计算出它们的直线积分：

  $$\begin{align} \iint\limits_D\left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)dA &= \iint\limits_{D'}\left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)dA + \iint\limits_{D''}\left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)dA \\&= \int_{\partial D'}Pdx + Qdy + \int_{\partial D''}Pdx + Qdy \end{align}$$

  两个区域的公共有向曲线形状相同、方向相反，因此将它们相加，我们可以得到：

  $$\iint\limits_D\left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)dA = \int_{C_1\cup C_2}Pdx + Qdy = \int_CPdx + Qdy$$

  这就是对区域 $D$ 的格林公式。

保守向量场判定定理的证明

设 $\mathbf F = P\mathbf i + Q\mathbf j$ 是在开连通区域 $R$ 内有定义的向量场，其中 $P$ 和 $Q$ 均在 $R$ 内有一阶偏导数，且

$$\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}\qquad\text{在 $R$ 内都成立}$$

• $C$ 为在 $R$ 内的简单闭合曲线， $D$ 为 $C$ 所围成的简单连通区域，则由格林公式可知

  $$\int_C \mathbf F\cdot d\mathbf r = \int_{\partial D}Pdx + Qdy = \iint\limits_D\left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dA = 0$$

  因此 $\mathbf F$ 的直线积分路径无关， $\mathbf F$ 是一个保守向量场。

• 对于非简单闭合曲线所围成的区域，其可以被分成有限个简单连通区域的并，则也可以通过格林公式证明 $\mathbf F$ 的直线积分路径无关，而 $\mathbf F$ 是一个保守向量场。