Calculus笔记-16.3-直线积分基本定理

2024-05-27

Calculus笔记-16.3-直线积分基本定理

直线积分基本定理

引入

微积分基本定理可以写为
$\int_a^bF'(x)dx = F(b) - F(a) \tag{3.1}\label{微积分基本定理}$
其中 $F’$ 在区间 $[a, b]$ 上连续。
我们将 $\eqref{微积分基本定理}$ 称作净变化定理：变化率的积分等于净变化量。

若将对二元或三院函数 $f$ 的梯度向量 $\nabla f$ 看作 $f$ 的导数，则下列定理可以被看作直线积分的基本定理：

定理

$\text{令 $C$ 为向量值函数 $\mathbf r(t),\ a\le t\le b$ 所确定的光滑曲线， $f$ 为梯度向量 $\nabla f$ 在 $C$ 上连续的二元或三元可导函数，则}\\ \int_Cf\cdot d\mathbf r = f(\mathbf r(b)) - f(\mathbf r(a)) \tag{3.2}\label{直线积分基本定理}$

定理 $\eqref{直线积分基本定理}$ 说明，我们可以在只知道 $f$ 分别在曲线 $C$ 的起点和终点的值的情况下求得其梯度场的直线积分。也就是说， $\nabla f$ 的直线积分等于 $f$ 的净变化量。
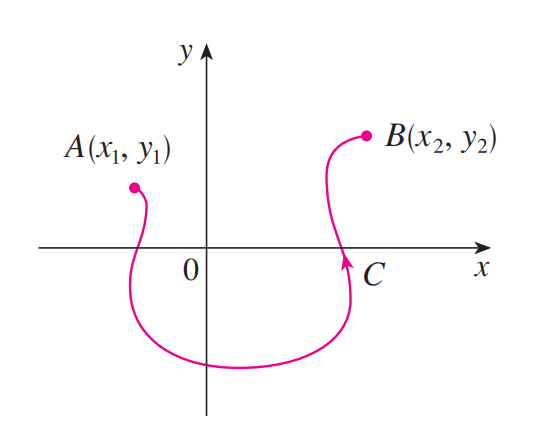
若 $f$ 是二元函数，且 $C$ 是起点为 $A(x_1, y_1)$ ，终点为 $B(x_2, y_2)$ 的平面曲线（如上图），则定理 $\eqref{直线积分基本定理}$ 变为
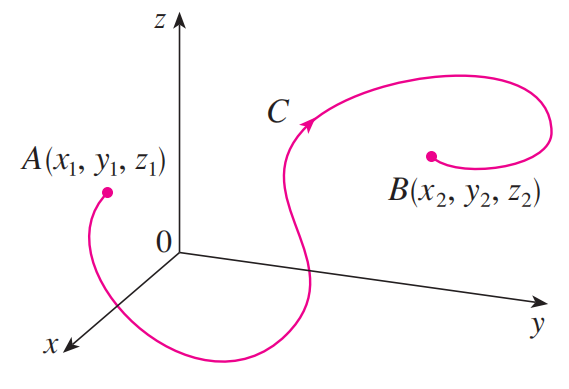
$\int_C\nabla f\cdot d\mathbf r = f(x_2, y_2) - f(x_1, y_1)\text{；}$
若 $f$ 是三元函数，且 $C$ 是起点为 $A(x_1, y_1, z_1)$ ，终点为 $B(x_2, y_2, z_2)$ 的空间曲线（如上图），则定理 $\eqref{直线积分基本定理}$ 变为
$\int_C\nabla f\cdot d\mathbf r = f(x_2, y_2, z_2) - f(x_1, y_1, z_1)\text{。}$

证明

$\begin{align} \int_C\nabla f\cdot d\mathbf r &= \int_a^b\nabla f(\mathbf r(t))\cdot \mathbf r'(t)dt \\&= \int_a^b\left( \frac{\partial f}{\partial x}\frac{dx}{dt} + \frac{\partial f}{\partial y}\frac{dy}{dt} + \frac{\partial f}{\partial z}\frac{dz}{dt} \right)\\&= \int_a^b\frac d{dt}f(\mathbf r(t))dt\qquad\text{(链式法则)} \\&= f(\mathbf r(b)) - f(\mathbf r(a))\qquad\text{(微积分基本定理)}. \end{align}$

该定理对由有限条光滑的曲线所组成的曲线 $C$ 也成立。

路径无关(independent of path)

引入

设 $C_1$ 和 $C_2$ 是两条有着相同起点 $A$ 和终点 $B$ 的（分段）光滑曲线（路径）。

一般来说， $\int_{C_1}\mathbf F\cdot d\mathbf r\ne\int_{C_2}\mathbf F\cdot d\mathbf r$ ，但从定理 $\eqref{直线积分基本定理}$ 可知，在 $\nabla f$ 连续时，
$\int_{C_1}\nabla f\cdot d\mathbf r = \int_{C_2}\nabla f\cdot d\mathbf r.$
即，保守向量场的直线积分只由曲线的起点和终点决定。

定义

一般来说，若 $\mathbf F$ 是在定义域 $D$ 内连续的向量场，若 $\int_{C_1}\mathbf F\cdot d\mathbf r = \int_{C_2}\mathbf F\cdot d\mathbf r$ 对于 $D$ 内任意两条起点和终点分别相同的路径 $C_1$ 和 $C_2$ 成立，则我们称直线积分 $\int_C\mathbf F\cdot d\mathbf r$ 路径无关。

路径无关的判定定理

如上图，如果一条曲线的起点与终点重合，则我们称其为闭合(closed)曲线，即 $\mathbf r(b) = \mathbf r(a)$ 。

定理

$\text{ $\int_C\mathbf F\cdot d\mathbf r$ 在 $D$ 内路径无关，当且仅当 $\int_C\mathbf F\cdot d\mathbf r = 0$ 对任意 $D$ 内的闭合路径 $C$ 成立。 } \tag{3.3}\label{路径无关判定定理}$

证明

充分性

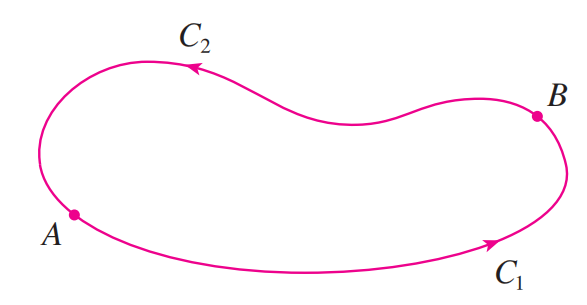
若 $\int_C\mathbf F\cdot d\mathbf r$ 在 $D$ 内路径无关，且 $C$ 是 $D$ 内的任意一条闭合路径，则我们可以在 $C$ 内任意选择两个点 $A$ 和 $B$ ，并将 $C$ 视为由从 $A$ 到 $B$ 的路径 $C_1$ 和从 $B$ 到 $A$ 的路径 $C_2$ 组成的路径（如上图）。则
$\int_C\mathbf F\cdot d\mathbf r = \int_{C_1}\mathbf F\cdot d\mathbf r + \int_{C_2}\mathbf F\cdot d\mathbf r = \int_{C_1}\mathbf F\cdot d\mathbf r - \int_{-C_2}\mathbf F\cdot d\mathbf r = 0.$
必要性

若对 $D$ 内的所有闭合路径 $C$ 都有 $\int_C\mathbf F\cdot d\mathbf r = 0$ ，取任意两条从 $A$ 到 $B$ 的路径 $C_1$ 和 $C_2$ ，并定义 $C$ 为由 $C_1$ 和 $-C_2$ 连接而成的曲线，则
$0 =\int_C\mathbf F\cdot d\mathbf r = \int_{C_1}\mathbf F\cdot d\mathbf r + \int_{-C_2}\mathbf F\cdot d\mathbf r = \int_{C_1}\mathbf F\cdot d\mathbf r - \int_{C_2}\mathbf F\cdot d\mathbf r$
，因此 $\int_{C_1}\mathbf F\cdot d\mathbf r = \int_{C_2}\mathbf F\cdot d\mathbf r$ 。

因此我们知道，任何保守向量场 $\mathbf F$ 是路径无关的，则对于任何闭合路径有 $\int_C\mathbf F\cdot d\mathbf r = 0$ 。其物理意义为保守力场在闭合曲线路径上所做的功为 $0$ 。

路径无关与保守向量场

下列定理证明了路径无关的向量场一定是保守向量场。

定理

$\text{设 $\mathbf F$ 是在开连通区间 $D$ （ $D$ 内不包含任何其边界点）内连续的向量场，}\\\text{若 $\int_C\mathbf F\cdot d\mathbf r$ 在 $D$ 内路径无关，则 $\mathbf F$ 为 $D$ 内的保守向量场，即存在 $f$ 使得 $\nabla f = \mathbf F$ 。} \tag{3.4}\label{路径无关向量场唯一性定理}$

证明

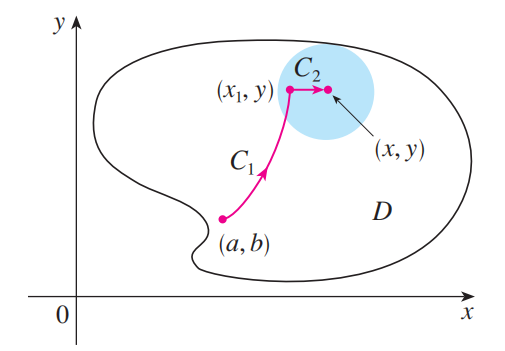
如图，设 $\int_C\mathbf F\cdot d\mathbf r = \int_{C_1}\mathbf F\cdot d\mathbf r + \int_{C_2}\mathbf F\cdot d\mathbf r$ ，令 $f(x, y) = \int_{(a, b)}^{(x, y)}\mathbf F\cdot d\mathbf r$ ，则

$f(x, y) = \int_{(a, b)}^{(x_1, y)}\mathbf F\cdot d\mathbf r + \int_{(x_1, y)}^{(x, y)}\mathbf F\cdot d\mathbf r$

该式右边的第一项和 $x$ 无关，则

$\frac \partial{\partial x}f(x, y) = \frac\partial{\partial x}0 + \frac \partial{\partial x}\int_{(x_1, y)}^{(x, y)}\mathbf F\cdot d\mathbf r$

将 $\mathbf F = P\mathbf i + Q\mathbf j$ 代入，则

$\begin{align} \frac \partial{\partial x}f(x, y) &= \frac \partial{\partial x} \int_{(x_1, y)}^{(x, y)}Pdx + Qdy \\&= \frac\partial{\partial x}\int_{x_1}^xP(t, y)dt \\&= P(x, y) \end{align}$

利用同样的方法我们也可以证明

$\frac \partial{\partial y}f(x, y) = Q(x, y)$

则 $\mathbf F = P\mathbf i + Q\mathbf j = \frac {\partial f}{\partial x}\mathbf i + \frac {\partial f}{\partial y}\mathbf j = \nabla f$ ，$\mathbf F$ 为保守向量场。

现在的问题是，如何确定一个向量场是否是保守向量场？

保守向量场与分量偏导数的关系（充分性）

设 $\mathbf F = P\mathbf i + Q\mathbf j$ 是保守向量场，其中 $P$ 和 $Q$ 都有连续一阶偏导数，则存在 $f$ 使得 $\mathbf F = \nabla f$ ，即：

$P = \frac{\partial f}{\partial x}\quad\text{且}\quad Q = \frac{\partial f}{\partial y}$

则由克莱罗公式可知

$\frac{\partial P}{\partial y} = \frac{\partial^2 f}{\partial y\partial x} = \frac{\partial^2 f}{\partial x\partial y} = \frac{\partial Q}{\partial x}.$

定理

$\text{若 $\mathbf F(x, y) = P(x, y)\mathbf i + Q(x, y)\mathbf j$ 是一个保守向量场，}\\\text{其中$P$ 和 $Q$ 在定义域 $D$ 上由一阶偏导数，则在整个 $D$ 内有}\\ \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}. \tag{3.5}\label{保守向量场与分量偏导数的充分性关系}$

保守向量场与分量偏导数的关系（必要性）

$\eqref{保守向量场与分量偏导数的充分性关系}$ 的逆定理只对特殊的区域成立。

简单曲线(simple curve)是不与自身相交的曲线,上图说明了哪些曲线是简单闭合曲线(Simple Closed Curve)。

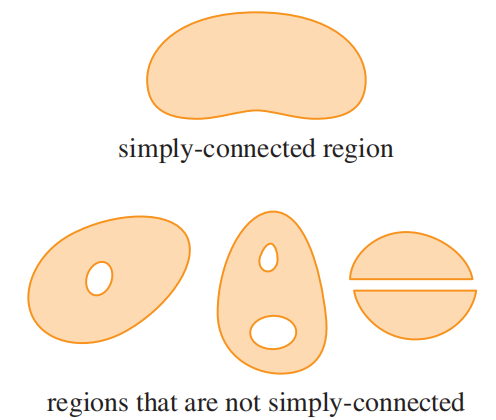
简单连通区域(simply-connected region)是指所有 $D$ 内的简单闭合曲线都只包含 $D$ 内的点的区域。简单来说，简单连通区域没有洞，而且不能存在两个分离的片段。

对于简单连通区域，我们可以得到定理 $\eqref{保守向量场与分量偏导数的充分性关系}$ 的部分逆定理：

定理

$\text{设 $\mathbf F = P\mathbf i + Q\mathbf j$ 为在开放简单连通区域 $D$ 上的向量场，}\\\text{设 $P$ 和 $Q$ 都存在一阶连续偏导数，则当}\\ \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x} \\ \text{在 $D$ 内都成立时， $\mathbf F$ 为保守向量场。} \tag{3.6}\label{保守向量场与分量偏导数的必要性关系}$

其证明在格林公式一节中给出。

求出 $f$

方法一

设存在 $f$ 使得 $\mathbf F = \nabla f$ ，则

若 $\mathbf F = P(x, y)\mathbf i + Q(x, y)\mathbf j$ ，则 $f_x = P(x, y)\qquad f_y = Q(x, y)$ 对 $P(x, y)$ 求积分，则 $f = \int P(x, y)dx + g(y) \tag{3.7}\label{f1}$ 两边对 $y$ 求导，则 $f_y = \frac\partial{\partial y}\int P(x, y)dx + g'(y)= Q(x, y)$ 则 $\begin{align} g'(y) &= Q(x, y) - \frac\partial{\partial y}\int P(x, y)dx \\ g(y)&= \int\left[ Q(x, y) - \frac\partial{\partial y}\int P(x, y)dx \right] dy + C \end{align}$ 代入 $\eqref{f1}$ 得 $f = \int P(x, y)dx + \int\left[ Q(x, y) - \frac\partial{\partial y}\int P(x, y)dx \right] dy + C. \tag{3.8}\label{f2}$

方法二

由直线积分基本定理，我们知道

$\int_C\mathbf F\cdot d\mathbf r = f(\mathbf r(a)) - f(\mathbf r(b)) \tag{3.9}\label{直线积分基本定理2}$

将式 $\eqref{直线积分基本定理2}$ 反过来，我们得到：

$f(x, y) = \int_{(x_0, y_0)}^{(x, y)}\mathbf F\cdot d\mathbf r + f(x_0, y_0)$

由路径无关可知，我们可以选择下图中的曲线来简化求解：

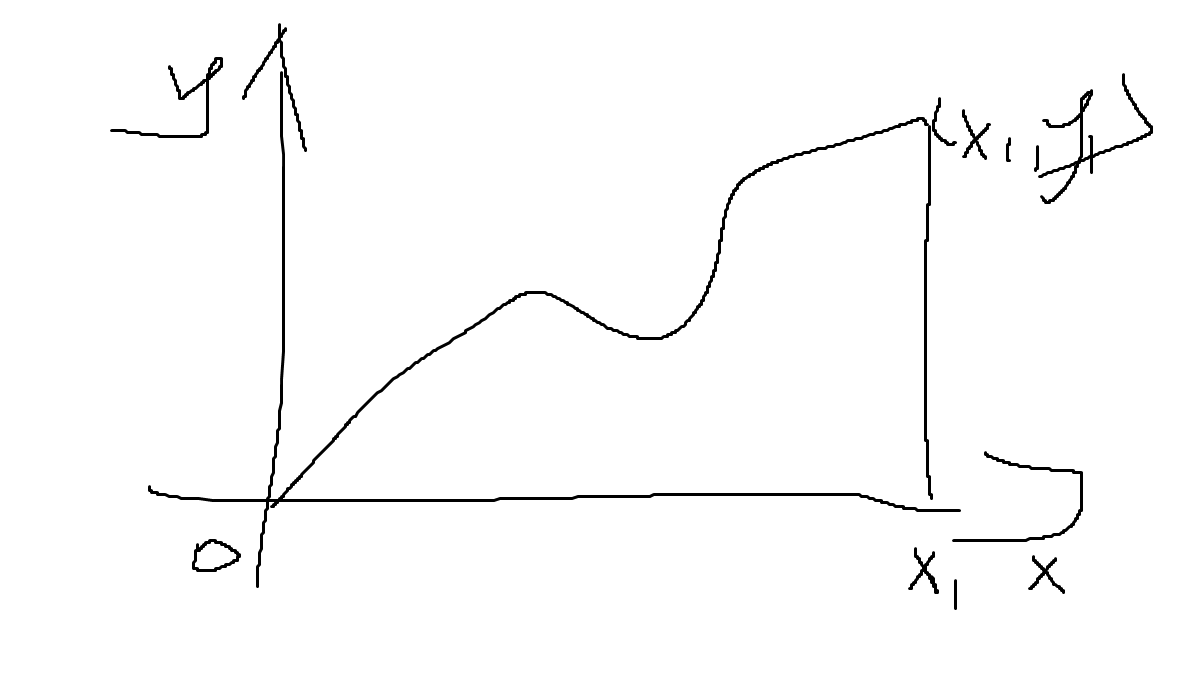
则

$\begin{align} f(x_1, y_1) &= \int_{(0, 0)}^{(x_1, 0)}Pdx + \int_{(x_1, 0)}^{(x_1, y_1)}Qdy \\&= \int_0^{x_1}P(x, 0)dx + \int_0^{y_1}Q(x_1, y)dy \\&= \left[\int P(x, 0)dx\right]_0^{x_1} + \left[\int Q(x_1, y)dy\right]_0^{y_1} \end{align}$

其中含有 $x_1,\ y_1$ 的项为自变量，其余为常数。

能量守恒定律

动能定理

将这章的思想应用到连续力场 $\mathbf F$ 将一个物体沿由 $\mathbf r(t),\ a\le t\le b$ ，所确定的路径 $C$ ，其中起点 $\mathbf r(a) = A$ ，终点 $\mathbf r(b) = B$ 上。

由牛顿第二定律可知， $C$ 上一点的力 $\mathbf F(\mathbf r(t))$ 与其加速度 $\mathbf a(t) = \mathbf r’’(t)$ 的关系由式

$\mathbf F(\mathbf r(t)) = m\mathbf r''(t)$

给出。

若物体在 $\mathbf F$ 的作用下由 $a$ 点移动到 $b$ 点，则

$\begin{align} W &= \int_C\mathbf F\cdot d\mathbf r \\&= \int_Cm\mathbf r''(t)\cdot\mathbf r'(t)dt \\&= \frac m2\int_C\frac d{dt}[\mathbf r'(t)\cdot\mathbf r'(t)]dt \\&= \frac m2\int_a^b\frac d{dt}|\mathbf r'(t)|^2dt \\&= \frac m2|\mathbf r'(b)|^2 - \frac m2|\mathbf r'(a)|^2 \end{align}$

因此

$W = \frac12m|\mathbf v(b)|^2 - \frac12m|\mathbf v(a)|^2 \tag{3.9}\label{动能定理1}$

其中 $\mathbf v = \mathbf r’$ 为速度矢量。

量 $\frac12m|\mathbf v(t)|^2$ 被称为物体的动能(kinetic energy)，因此我们可以将方程 $\eqref{动能定理1}$ 改写为

$W = K(B) - K(A) \tag{3.10}\label{动能定理2}$

式 $\eqref{动能定理2}$ 的物理含义是，力沿 $C$ 对物体所做的功等于物体在 $C$ 两端点的动能变化量。

能量守恒

我们进而假设力场 $\mathbf F$ 为保守力场，即存在 $f$ 满足 $\mathbf F = \nabla f$ 。在物理中，物体在点 $(x, y, z)$ 的势能(potential energy) $P(x, y, z) = - f(x, y, z)$ ，则 $\mathbf F = -\nabla P$ ，由定理 $\eqref{直线积分基本定理}$ 可知，

$W = \int_C\mathbf F\cdot d\mathbf r = -\int_C\nabla P\cdot d\mathbf r = -[P(\mathbf r(b)) - P(\mathbf r(a))] = P(A) - P(B)$

与 $\eqref{动能定理2}$ 比较，则

$P(A) + K(A) = P(B) + K(B)$

这说明物体在保守力场的作用下从点 $A$ 运动到另一点 $B$ 时，其势能和动能总和保持不变。这被称为能量守恒定律(Law of Conservation of Energy)，这就是为什么这样的向量场被称为保守向量场。