Calculus笔记-16.2-直线积分

2024-05-13

Calculus笔记-16.2-直线积分

直线积分

引入

如图

考虑由参数方程
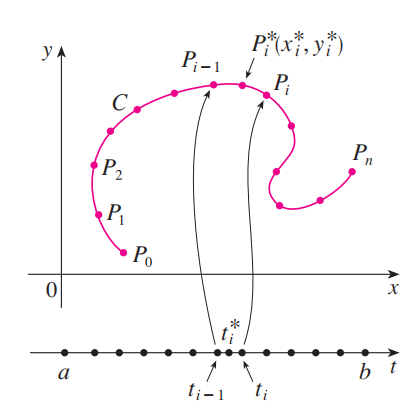
$x = x(t)\qquad y = y(t)\qquad a\le t\le b \tag{2.1}\label{参数方程}$
所确定的平面曲线 $C$ ，它也可以用向量方程 $\mathbf r(t) = x(t)\mathbf i + y(t)\mathbf j$ 来表示。其中 $C$ 是一条平滑曲线，即 $\mathbf r’$ 连续且 $\mathbf r’(t)\ne\mathbf 0$ 。
将参数区间 $[a, b]$ 分成 $n$ 个等宽子区间 $[t_{i - 1}, t_i]$ ，令 $x_i = x(t_i)$ 且 $y_i = y(t_i)$ ，则对应的点 $P_i(x_i, y_i)$ 将 $C$ 分割成 $n$ 个子弧段，分别长 $\Delta s_1, \Delta s_2, \dots, \Delta s_n$ 。在第 $i$ 个子弧段中取采样点 $P_i^*(x_i^*, y_i^*)$ ，这个点对应 $[t_{i - 1}, t_i]$ 中的点 $t_i^*$ 。
令 $f$ 为定义域包括曲线 $C$ 的二元函数，和
$\sum_{i = 1}^nf(x_i^*, y_i^*)\Delta s_i$
的形式和黎曼和相似。我们可以将这些和进行求和，并给出直线积分的定义：

直线积分的定义

若 $f$ 在由 $\eqref{参数方程}$ 定义的曲线 $C$ 上有定义，则 $\boldsymbol f$ 沿 $\boldsymbol C$ 的直线积分(line integral of $\boldsymbol f$ along $\boldsymbol C$ )为
$\int_Cf(x, y)ds = \lim_{n\to\infty}\sum^n_{i = 1}f(x_i^*, y_i^*)\Delta s_i \tag{2.2}\label{直线积分1}$
如果这个极限存在的话。
从 $10.2$ 节我们知道， $C$ 的长度为
$L = \int_a^b \sqrt{ \left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 }dt \tag{2.3}\label{弧长公式}$
，则式 $\eqref{直线积分1}$ 也可写成
$\int_Cf(x, y)ds = \int_a^b f(x(t), y(t)) \sqrt{ \left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 }dt. \tag{2.4}\label{直线积分2}$
直线积分的值和 $t$ 的取值无关，因为它只与 $a$ 到 $b$ 的路程有关。
若 $s(t)$ 为 $C$ 在 $\mathbf r(a)$ 和 $\mathbf r(b)$ 之间的长度，则
$\frac{ds}{dt} = \sqrt{ \left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 }$
则
$ds = \sqrt{ \left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 }dt.$
在 $C$ 是从 $(a, 0)$ 到 $(b, 0)$ 的线段的特例中，以 $x$ 为参变量，我们可以将 $C$ 的参数方程写为： $x = x,\ y = 0,\ a\le x\le b$ ，则式 $\eqref{直线积分2}$ 变为
$\int_Cf(x, y)ds = \int_a^bf(x, 0)dx \tag{2.5}\label{单变量积分}$
，则直线积分在这种情况下退化为一般单变量积分(ordinary single integral)。
和一般单变量积分一样，我们将对正值函数的直线积分理解为面积。形式化地，若 $f(x, y)\ge 0$ ， $\int_Cf(x, y)ds$ 代表下图中的“围栏”的面积，其中底为 $C$ ，点 $(x, y)$ 上的高度为 $f(x, y)$ 。

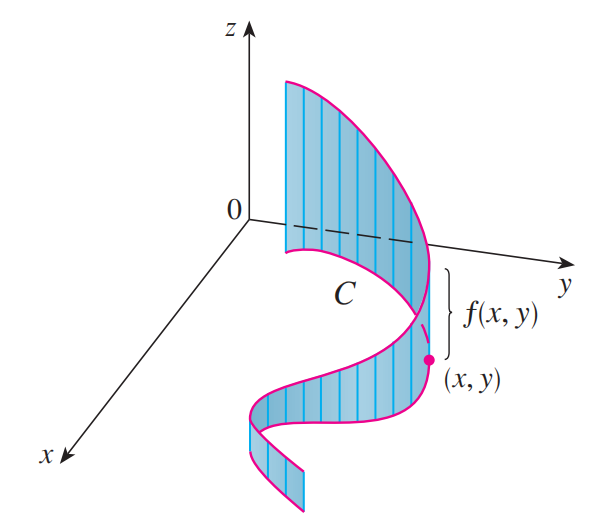
分段曲线的直线积分

若 $C$ 是一条分段平滑曲线(piecewise-smooth curve)，即 $C$ 是由有限条首尾相接的平滑曲线 $C_1, C_2, \dots, C_n$ 组成的曲线，则 $\int_Cf(x, y)ds = \int_{C_1}f(x, y)ds + \int_{C_2}f(x, y)ds + \dots + \int_{C_n}f(x, y)ds. \tag{2.6}\label{分段积分}$

物理上的应用

直线积分 $\int_Cf(x, y)ds$ 的物理意义由 $f$ 的物理意义来决定。

设 $\rho(x, y)$ 代表形状类似曲线 $C$ 的细线在点 $(x, y)$ 的线密度，则细线从 $P_{i - 1}$ 到 $P_i$ 的质量可以用 $\rho(x_i^*, y_i^*)\Delta s_i$ 来近似，细线的总质量可以用 $\sum\rho(x_i^*, y_i^*)\Delta s_i$ 来近似。将这个和取极限，我们可以得到曲线的质量(mass) $m$ ：
$m = \lim_{n\to\infty} \sum_{i = 1}^n \rho(x_i^*, y_i^*) \Delta s_i = \int_C\rho(x, y)ds. \tag{2.7}\label{质量}$
具有密度函数 $\rho$ 的细线的质心(center of mass)位于点 $(\bar x, \bar y)$ ，其中
$\bar x = \frac1m\int_Cx\rho(x, y)ds\qquad \bar y = \frac1m\int_Cy\rho(x, y)ds. \tag{2.8}\label{质心}$

对坐标的直线积分

将 $\Delta s_i$ 替换为 $\Delta x_i = x_i - x_{i - 1}$ 或 $\Delta y_i = y_i - y_{i - 1}$ ，则我们得到 $\boldsymbol f$ 沿 $\boldsymbol C$ 对 $\boldsymbol x$ 和 $\boldsymbol y$ 的直线积分(line integrals of $\boldsymbol f$ along $\boldsymbol C$ with respect to $\boldsymbol x$ and $\boldsymbol y$ )：
$\int_Cf(x, y)dx = \lim_{n\to\infty} \sum_{i = 1}^n f(x_i^*, y_i^*) \Delta x_i \tag{2.9}\label{对x的直线积分}$ $\int_Cf(x, y)dx = \lim_{n\to\infty} \sum_{i = 1}^n f(x_i^*, y_i^*) \Delta x_i \tag{2.10}\label{对y的直线积分}$
相对地，我们将积分 $\int_Cf(x, y)ds$ 称为对弧长的直线积分。
我们同样可以用 $t$ 来对对坐标的直线积分求值：
$\int_Cf(x, y)dx = \int_Cf(x(t), y(t))x'(t)dt \\ \int_Cf(x, y)dy = \int_Cf(x(t), y(t))y'(t)dt \tag{2.11}\label{对t的直线积分}$
对 $x$ 和 $y$ 的直线积分经常同时出现。习惯上将其缩写为：
$\int_CP(x, y)dx + \int_CQ(x, y)dy = \int_CP(x, y)dx + Q(x, y)dy. \tag{2.12}\label{对坐标直线积分的缩写}$
起点为 $\mathbf r_0$ ，终点为 $\mathbf r_1$ 的线段可以由向量表示法
$\mathbf r(t) = (1 - t)\mathbf r_0 + t\mathbf r_1\qquad 0\le t\le 1 \tag{2.13}\label{线段的向量表示法}$
给出。

直线积分的性质

当我们对所求直线积分给出参数化 $x = x(t),\ y = y(t),\ a\le t\le b$ ，则这种参数化确定了一种方向，如下图：

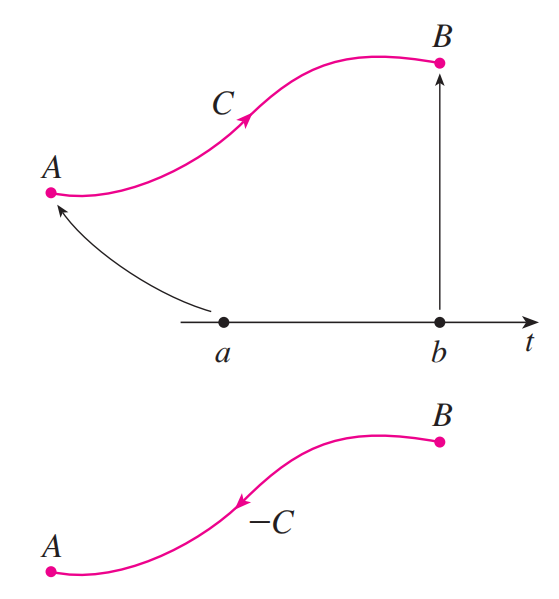
其中正方向代表了 $t$ 增加的方向。

若我们认为 $-C$ 代表了 $C$ 的反方向，则我们有
$\int_{-C}f(x, y)dx = -\int_Cf(x, y)dx\qquad \int_{-C}f(x, y)dy = -\int_Cf(x, y)dy$
但当我们对弧长求积分时，则有：
$\int_{-C}f(x, y)ds = \int_Cf(x, y)ds$
因为无论方向怎么变化， $\Delta s$ 的值总是正的。

空间中的直线积分

设 $C$ 是由参数方程
$x = x(t)\qquad y = y(t)\qquad z = z(t)\qquad a\le t\le b$
或向量方程 $\mathbf r(t) = x(t)\mathbf i + y(t)\mathbf j + z(t)\mathbf k$ 所确定的空间曲线。若 $f$ 是在积分区域 $C$ 中连续的三元函数，则定义 $\boldsymbol f$ 沿 $\boldsymbol C$ 的（对弧长）直线积分(line integral of $\boldsymbol f$ along $\boldsymbol C$ )为：
$\int_Cf(x, y, z)ds = \lim_{n\to\infty} \sum_{i = 1}^nf(x_i^*, y_i^*, z_i^*)\Delta s_i \tag{2.14}\label{空间直线积分1}$
我们用和式 $\eqref{直线积分2}$ 相似的方法来对其求值：
$\int_Cf(x, y, z)ds = \int_a^bf(x(t), y(t), z(t)) \sqrt{ \left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 + \left(\frac{dz}{dt}\right)^2 }dt \tag{2.15}\label{空间直线积分2}$
注意到积分 $\eqref{直线积分2}$ 和 $\eqref{空间直线积分2}$ 都可以写成更精简的形式：
$\int_a^bf(\mathbf r(t)) |\mathbf r'(t)| dt$
在 $f(x, y, z) = 1$ 的特例中，我们得到：
$\int_Cds = \int_a^b|\mathbf r'(t)|dt = L$
其中 $L$ 为曲线 $C$ 的弧长。
沿 $C$ 对 $x$ , $y$ , $z$ 的直线积分也可以被分别定义出来。比如：
$\begin{align} \int_Cf(x, y, z)dz &= \lim_{n\to\infty}\sum_{i = 1}^n f(x_i^*, y_i^*, z_i^*)\Delta z_i \\&= \int_a^bf(x(t), y(t), z(t))z'(t)dt \end{align}$
因此，我们可以通过将 $(x, y, z, dx, dy, dz)$ 都以参变量 $t$ 来表示的方式来计算
$\int_CP(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz. \tag{2.16}\label{对坐标的空间直线积分}$

向量场的直线积分

引入

如何求变化力在沿曲线运动的过程中所做的功？

从 $6.4$ 节中，我们知道，由变化力在粒子沿 $x$ 轴由 $a$ 运动到 $b$ 时所做的功为 $W = \int_a^bf(x)dx$ ；从 $12.3$ 节中，我们知道，由不变力 $\mathbf F$ 在空间中从点 $P$ 运动到另一点 $Q$ 时所做的功为 $W = \mathbf F\cdot\mathbf D$ ，其中 $\mathbf D = \overrightarrow{PQ}$ 是位移矢量。
设 $\mathbf F = P\mathbf i + Q\mathbf j + R\mathbf k$ 是在 $\mathbb R^3$ 中连续的力场，且通过移动粒子沿平滑的曲线 $C$ 做功。

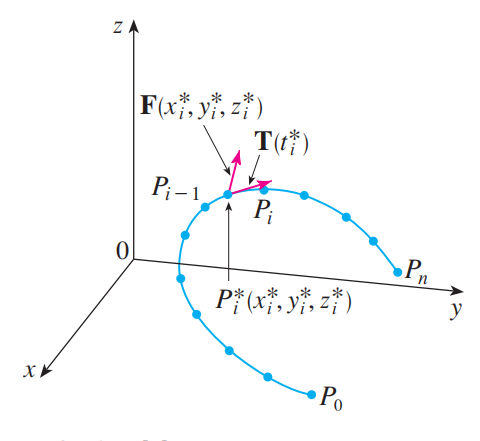
如上图，通过将参变量区间 $[a, b]$ 分成等长的子区间，我们将 $C$ 分割成子弧段 $P_{i - 1}P_i$ ，每一个长 $\Delta s_i$ 。在第 $i$ 个子区间对应参变量值 $t_i^*$ 选择采样点 $P_i^*(x_i^*, y_i^*, z_i^*)$ 。若 $\Delta s_i$ 足够小，则粒子在从 $P_{i - 1}$ 到 $P_i$ 的运动过程可以用在 $P_i^*$ 的单位切向量 $\mathbf T(t_i^*)$ 的方向来近似。因此力 $\mathbf F$ 在将粒子由 $P_{i - 1}$ 推动到 $P_i$ 的过程中所做的功可以近似为
$\mathbf F(x_i^*, y_i^*, z_i^*)\cdot [\Delta s_i\mathbf T(t_i^*)] = [\mathbf F(x_i^*, y_i^*, z_i^*)\cdot \mathbf T(t_i^*)]\Delta s_i$
，而将粒子沿曲线 $C$ 推动时所做的总功可以近似为
$\sum_{i = 1}^n [\mathbf F(x_i^*, y_i^*, z_i^*)\cdot \mathbf T(x_i^*, y_i^*, z_i^*)]\Delta s_i \tag{2.17}\label{功的黎曼和}$
，其中 $\mathbf T(x, y, z)$ 为点 $(x, y, z)$ 在 $C$ 上的单位切向量。我们可以直观地认为这个近似在 $n$ 变大时会变得更好。因此我们将力场 $\mathbf F$ 所做的功(work) $W$ 定义为黎曼和 $\eqref{功的黎曼和}$ 的极限，即：
$W = \int_C\mathbf F(x, y, z)\cdot \mathbf T(x, y, z)ds = \int_C\mathbf F\cdot\mathbf Tds. \tag{2.18}\label{功的定义}$
式 $\eqref{功的定义}$ 表示功就是力的切向分量对弧长的积分。
如果曲线由向量方程 $\mathbf r(t) = x(t)\mathbf i + y(t)\mathbf j + z(t)\mathbf k$ 给出，则 $\mathbf T(t) = \mathbf r’(t) / |\mathbf r’(t)|$ ，则用式 $\eqref{空间直线积分2}$ 我们可以将 $\eqref{功的定义}$ 改写为
$W = \int_a^b\mathbf F(\mathbf r(t))\cdot \frac{\mathbf r'(t)}{|\mathbf r'(t)|} |\mathbf r'(t)|dt = \int_a^b\mathbf F(r(t))\cdot\mathbf r'(t)dt.$
这个积分通常缩写为 $\int_C\mathbf F\cdot d\mathbf r$ ，也会在物理的其他领域中出现。因此我们就可以得出以下关于任何向量场的的定义：

向量场直线积分的定义

令 $\mathbf F$ 为由向量方程 $\mathbf r(t), a\le t\le b$ 所确定，在平滑曲线 $C$ 上有定义的连续向量场，则 $\mathbf F$ 沿 $\boldsymbol C$ 的直线积分(line integral of $\mathbf F$ along $\boldsymbol C$ ) 为： $\int_C\mathbf F\cdot d\mathbf r = \int_a^b\mathbf F(\mathbf r(t))\cdot \mathbf r'(t)dt = \int_C\mathbf F\cdot\mathbf Tds. \tag{2.19}\label{向量场直线积分的定义}$ 其中 $\mathbf F(\mathbf r(t))$ 为向量场 $\mathbf F(x(t), y(t), z(t))$ 的缩写， $d\mathbf r = \mathbf r’(t)dt$ 。

向量场和数量场的直线积分

设在 $\mathbb R^3$ 上的向量场 $\mathbf F$ 由分量式方程 $\mathbf F = P\mathbf i + Q\mathbf j + R\mathbf k$ 给出，则由定义 $\eqref{向量场直线积分的定义}$ 可知 $\begin{align} \int_C\mathbf F\cdot d\mathbf r &= \int_a^b\mathbf F(x, y, z)\cdot \mathbf r'(t)dt \\&= \int_a^b\mathbf F( P\mathbf i + Q\mathbf j + R\mathbf k )\cdot (x'(t)\mathbf i + y'(t)\mathbf j + z'(t)\mathbf k)dt \\&= \int_a^b[ P(x(t), y(t), z(t))x'(t) + Q(x(t), y(t), z(t))y'(t) + R(x(t), y(t), z(t))z'(t) ]dt \end{align}$ 而最后一行恰恰是 $\eqref{对坐标的空间直线积分}$ 中的直线积分，则有： $\int_C\mathbf F\cdot d\mathbf r = \int_a^b Pdx + Qdy + Rdz\qquad\text{其中 } \mathbf F = P\mathbf i + Q\mathbf j + R\mathbf k.$