Calculus笔记-15.9-多重积分的换元法

Calculus笔记-15.9-多重积分的换元法

二重积分的换元法

引入

考虑由从 $uv$ 平面到 $xy$ 平面的变换(transformation) $T$ 给出的变换：

$$T(u, v) = (x, y)$$

其中 $x$ 、 $y$ 和 $u$ 、 $v$ 的关系由

$$x = g(u, v)\qquad y = h(u, v) \tag{9.1}\label{xyuv}$$

或

$$x = x(u, v)\qquad y = y(u, v)$$

确定。通常假设 $T$ 是一个 $\mathbf{C^1}$ 变换(transformation)，即 $g$ 和 $h$ 都有一阶导数。

• 当变换 $T$ 的定义域和值域都为 $\mathbb{R}^2$ 时，它是一个函数。
• 当 $T(u_1, v_1) = (x_1, y_1)$ 时，点 $(x_1, y_1)$ 被称为点 $(u_1, v_1)$ 的图像(image)。
• 当没有两个点的图像相同时， $T$ 是一个一一对应(one-to-one)的变换。

下图说明了变换 $T$ 对 $uv$ 平面上的区域 $S$ 的作用。

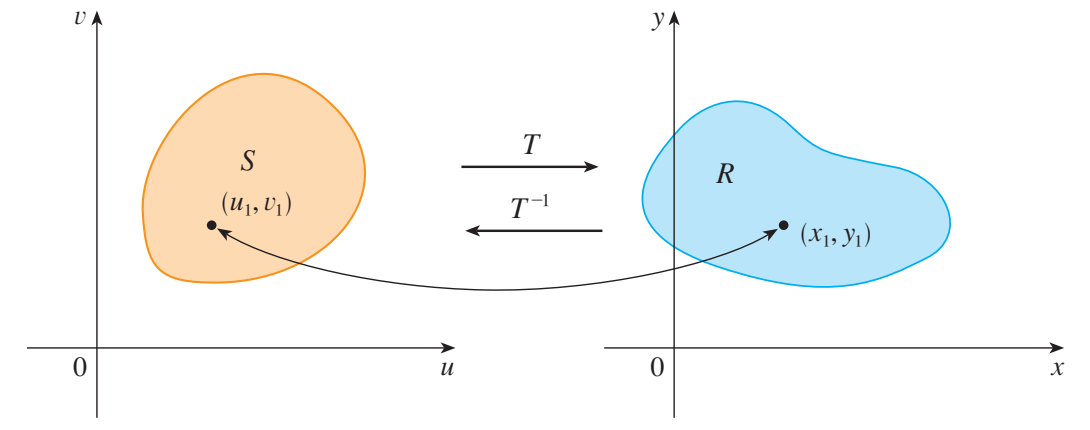
$T$ 将 $S$ 变换为 $xy$ 平面上的区域 $R$ ，这个区域被称为 $\mathbf{S}$ 的图像(the image of $\mathbf{S}$ )，包括了 $S$ 上所有点的图像。

如果 $T$ 是一个一一对应的变换，则它有从 $xy$ 平面到 $uv$ 平面的逆变换(inverse transformation) $T^{-1}$ ，并可以利用它来解出式 $\eqref{xyuv}$ ，从而用 $x$ 和 $y$ 来表示 $u$ 和 $v$ ：

$$u = G(x, y)\qquad v = H(x, y)$$

观察变量的变换是如何影响二重积分的。从一个在 $uv$ 平面内，左下角为 $(u_0, v_0)$ ，边长分别为 $\Delta u$ 和 $\Delta v$ 的矩形 $S$ 开始（如下图）：

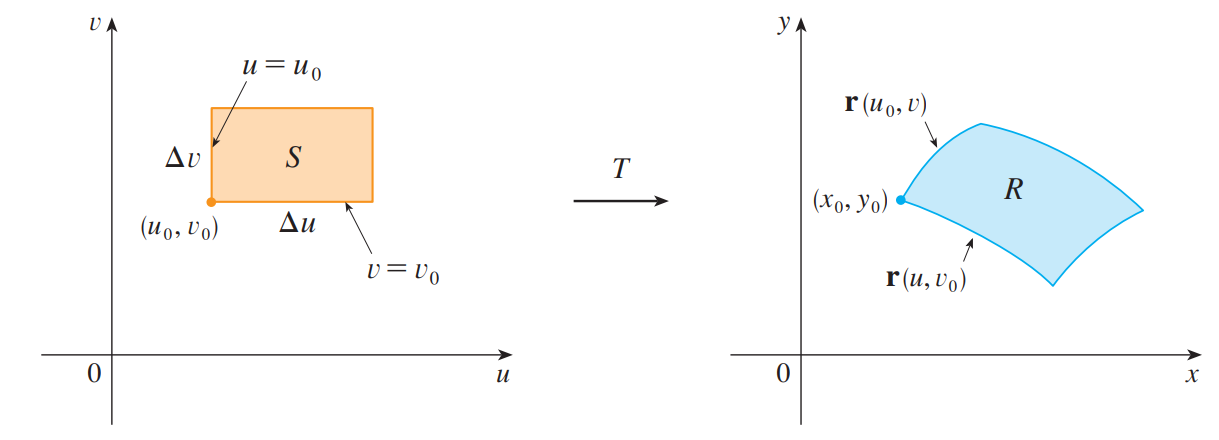
$S$ 的图像是一块在 $xy$ 平面内的区域 $R$ ，它的一个边界点是 $(x_0, y_0) = T(u_0, v_0)$ 。向量

$$\mathbf{r}(u, v) = g(u, v)\mathbf{i} + h(u, v)\mathbf{j}$$

是点 $(u, v)$ 图像的位置矢量。

$S$ 靠下一侧的方程是 $v = v_0$ ，它的图像曲线由向量值函数 $\mathbf{r}(u, v_0)$ 确定。这条图像曲线在 $(x_0, y_0)$ 的切向量为：

$$\mathbf{r}_u = g_u(u_0, v_0)\mathbf{i} + h_u(u_0, v_0)\mathbf{j} = \frac{\partial x}{\partial u}\mathbf{i} + \frac{\partial y}{\partial u}\mathbf{j}$$

相似地， $S$ 左侧的图像曲线（即 $u = u_0$ ）在 $(x_0, y_0)$ 的切线为

$$\mathbf{r}_v = g_v(u_0, v_0)\mathbf{i} + h_v(u_0, v_0)\mathbf{j} = \frac{\partial x}{\partial v}\mathbf{i} + \frac{\partial y}{\partial v}\mathbf{j}$$

我们可以用由割向量

$$\mathbf a = \mathbf r(u_0 + \Delta u, v_0) - \mathbf r(u_0, v_0)\qquad \mathbf b = \mathbf r(u_0, v_0 + \Delta v) - \mathbf r(u_0, v_0)$$

来近似区域 $R = T(S)$ 的图像，如下图所示：

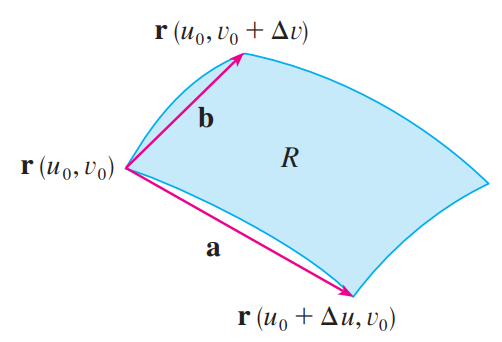
因为

$$\mathbf r_u = \lim_{\Delta u\to 0} \frac{ \mathbf r(u_0 + \Delta u, v_0) - \mathbf r(u_0, v_0) } {\Delta u}$$

所以

$$\mathbf r(u_0 + \Delta u, v_0) - \mathbf r(u_0, v_0)\approx \Delta u\mathbf r_u$$

相似地，

$$\mathbf r(u_0, v_0 + \Delta v) - \mathbf r(u_0, v_0)\approx \Delta v\mathbf r_v$$

这意味着我们可以用向量 $\Delta u\mathbf r_u$ 和 $\Delta v\mathbf r_v$ 所确定的平行四边形来近似 $R$ （如下图）：

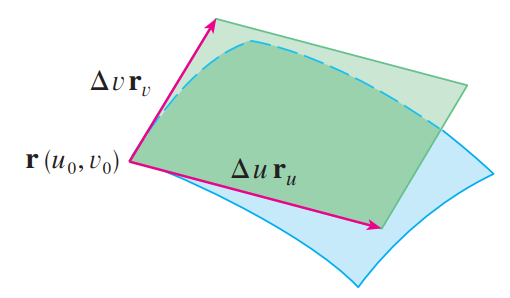
则我们可以用平行四边形的面积来近似 $R$ 的面积：

$$|(\Delta u\mathbf r_u)\times (\Delta v\mathbf r_v)| = |\mathbf r_u\times\mathbf r_v| \Delta u\Delta v \tag{6.2}\label{近似面积1}$$

将叉乘展开，我们得到：

$$\mathbf r_u\times\mathbf r_v = \begin{vmatrix} \mathbf i & \mathbf j & \mathbf k \\ \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} & 0 \\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} & 0 \\ \end{vmatrix} = \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u}\\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v}\\ \end{vmatrix}\mathbf k = \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u}& \frac{\partial y}{\partial v}\\ \end{vmatrix}\mathbf k$$

结果中的行列式被叫做这个变换的雅各比式(Jacobian)，由一个特定的符号来表示。

雅各比式的定义

由 $x = g(u, v)$ 和 $y = h(u, v)$ 确定的变换 $T$ 的雅各比式为：

$$\frac{\partial(x, y)}{\partial(u, v)} = \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u}& \frac{\partial y}{\partial v}\\ \end{vmatrix} = \frac{\partial x}{\partial u} \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u} \tag{6.3}\label{雅各比式}$$

将这个符号代入式 $\eqref{近似面积1}$ ，我们可以给出对 $R$ 的面积 $\Delta A$ 的近似：

$$\Delta A\approx \left| \frac{\partial(x, y)}{\partial(u, v)} \right|\Delta u\Delta v \tag{6.4}\label{近似面积2}$$

其中雅各比式的值在 $(u_0, v_0)$ 求得。

用雅各比式来计算二重积分

下一步，我们将 $uv$ 平面中的区域 $S$ 分割成矩形 $S_{ij}$ ，将它们在 $xy$ 平面中的图像设为 $R_{ij}$ （如下图）：

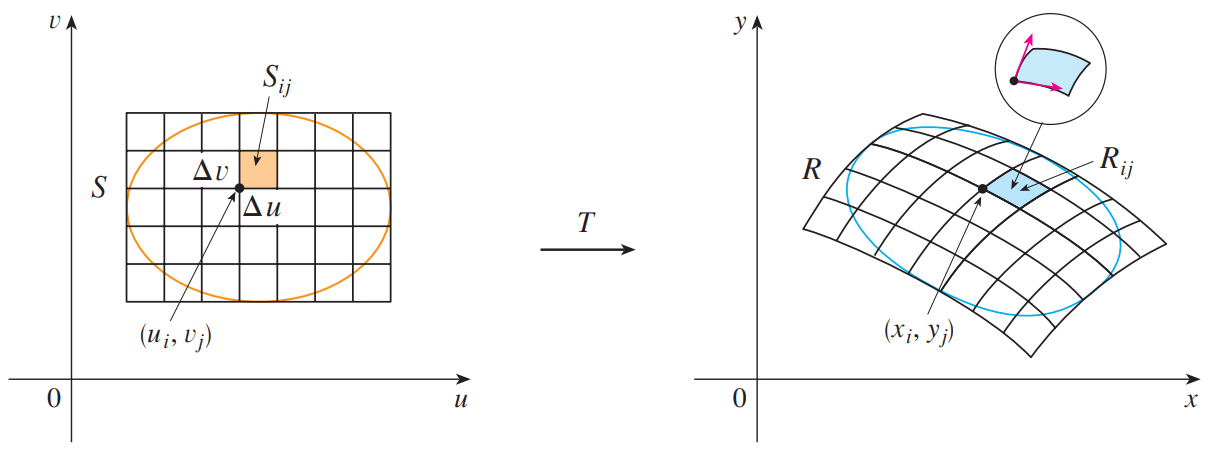
将近似面积 $\eqref{近似面积2}$ 代入每一个 $R_{ij}$ ，我们可以近似求得 $f$ 对 $R$ 的二重积分：

$$\begin{align} \iint\limits_Rf(x, y)dA &\approx \sum_{i = 1}^m\sum_{j = 1}^n f(x_i, y_j)\Delta A \\&\approx \sum_{i = 1}^m\sum_{j = 1}^n f(g(u_i, v_j), h(u_i, v_j)) \left| \frac{\partial(x, y)}{\partial(u, v)} \right|\Delta u\Delta v \end{align}$$

其中雅各比式的值在 $(u_i, v_j)$ 求得。

注意到这个和即为二重积分

$$\iint\limits_R f(g(u, v), h(u, v)) \left| \frac{\partial(x, y)}{\partial(u, v)} \right|\ du\ dv$$

的黎曼和。

上述论证表明以下定理是正确的（严谨证明需要用到高级微积分的知识）：

二重积分换元定理

$$\text{设 $T$ 是雅各比式非零的 $C^1$ 变换，且 $T$ 将 $uv$ 平面中的区域 $S$ 映射到 $xy$ 平面中的区域 $R$ 。}\\ \text{设 $f$ 在 $R$ 上连续，且 $R$ 和 $S$ 为第一类或第二类二重积分区域。}\\ \text{设 $T$ 是除了在 $S$ 的边界上外都是一一对应的变换，则 }\\ \iint\limits_Rf(x, y)dA = \iint\limits_R f(x(u, v), y(u, v)) \left| \frac{\partial(x, y)}{\partial(u, v)} \right|\ du\ dv \tag{6.5}\label{二重积分换元法}$$

定理 $\eqref{二重积分换元法}$ 的意思是，通过用 $u$ 和 $v$ 表示 $x$ 和 $y$ ，并令

$$dA = \left| \frac{\partial(x, y)}{\partial(u, v)} \right|\ du\ dv$$

来将对 $x$ 和 $y$ 的积分变换成对 $u$ 和 $v$ 的积分。

极坐标的二重积分公式

以极坐标为例子来说明定理 $\eqref{二重积分换元法}$ 的用法：

在极坐标中，从 $r\theta$ 平面到 $xy$ 平面的变换 $T$ 为：

$$x = g(r, \theta) = r\cos\theta \qquad y = h(r, \theta) = r\sin\theta$$

变换的几何含义如下图所示：

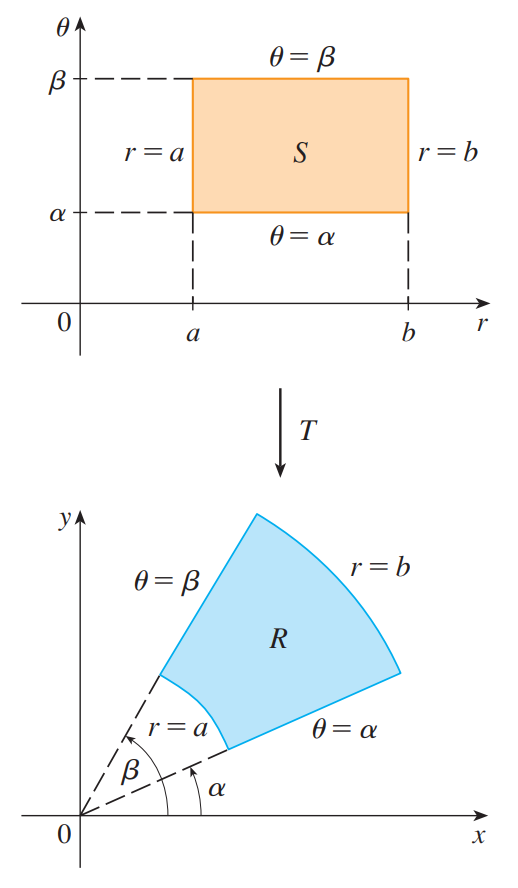
$T$ 将 $r\theta$ 平面中的一般矩形映射到 $xy$ 平面中的极矩形。

$T$ 的雅各比式为：

$$\frac{\partial(x, y)} {\partial(r, \theta)} = \begin{vmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\ \frac{\partial y}{\partial r}& \frac{\partial y}{\partial \theta}\\ \end{vmatrix} = \begin{vmatrix} \cos\theta & - r\sin\theta\\ \sin\theta& r\cos\theta\\ \end{vmatrix} = r\cos^2\theta + r\sin^2\theta = r > 0$$

代入 $\eqref{二重积分换元法}$ 得：

$$\iint\limits_Rf(x, y)\ dx\ dy = \int_\alpha^\beta\int_a^b f(r\cos\theta, r\sin\theta)r\ dr\ d\theta \tag{6.6}\label{极坐标的二重积分公式}$$

即极坐标的二重积分公式。

三重积分换元法

利用和 $\eqref{二重积分换元法}$ 类似的假设，我们可以得到如下关于三重积分的公式：

三重积分换元定理

$$\text{设 $T$ 为将 $uvw$ 平面中的区域 $S$ 映射到 $xyz$ 平面中的区域 $R$ 的变换，其关系为：}\\ x = g(u,v,w)\qquad y = h(u,v,w)\qquad z = k(u,v,w)\\ \text{则}\\ \iiint\limits_Rf(x, y, z)dV = \iiint\limits_R f(x(u, v, w), y(u, v, w), z(u, v, w)) \left| \frac{\partial(x, y, z)}{\partial(u, v, w)} \right|\ du\ dv\ dw\\ \text{其中}\\ \frac{\partial(x, y, z)}{\partial(u, v, w)} = \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w}\\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w}\\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w} \end{vmatrix}. \tag{6.7}\label{三重积分换元法}$$

球坐标的三重积分公式

• 我们使用球坐标

$$x = r\sin\phi\cos\theta\qquad y = r\sin\phi\sin\theta\qquad z = r\cos\phi \tag{6.8}\label{球坐标}$$

来表示和三维中的球面有关的坐标时十分便捷。

若我们将 $r$ , $\phi$ 和 $\theta$ 看作变量，则式 $\eqref{球坐标}$ 可以看作从 $r\phi\theta$ 空间到 $xyz$ 空间的一个变换。因此我们可以运用三重积分的换元法来将对 $xyz$ 的三重积分转换为对 $r\phi\theta$ 的三重积分。

计算雅各比式：

$$\begin{align} \frac{\partial(x, y, z)}{\partial(u, v, w)} &= \begin{vmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial\rho} & \frac{\partial x}{\partial\theta}\\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial\rho} & \frac{\partial y}{\partial\theta}\\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial\rho} & \frac{\partial z}{\partial\theta}\\ \end{vmatrix} \\&= \begin{vmatrix} \sin\phi\cos\theta & r\cos\phi\cos\theta & -r\sin\phi\sin\theta\\ \sin\phi\sin\theta & r\cos\phi\sin\theta & r\sin\phi\cos\theta\\ \cos\phi & -r\sin\phi & 0 \end{vmatrix} \\&= \cos\phi \left( r\sin\phi\cos\theta\cos\phi\sin\theta - r\cos\phi\cos\theta\sin\phi\sin\theta \right) + r\sin\phi \left( r\sin\phi\cos\theta\sin\phi\cos\theta + r\sin\phi\sin\theta\sin\phi\sin\theta \right) \\&= r^2\sin\phi \end{align}$$

所以

$$\left|\frac{\partial(x, y, z)}{\partial(u, v, w)}\right| = r^2\sin\phi$$

代入式 $\eqref{三重积分换元法}$ 得

$$\iiint\limits_Rf(x, y, z)dV = \iiint\limits_Rf(r\sin\phi\cos\theta, r\sin\phi\sin\theta, r\cos\theta)r^2\sin\phi\ drd\theta d\phi \tag{6.9}\label{球坐标的三重积分公式}$$

式 $\eqref{球坐标的三重积分公式}$ 即为球坐标的三重积分公式。