Calculus笔记-15.8-球坐标的三重积分

2024-05-06

Calculus笔记-15.8-球坐标的三重积分

球坐标系(Spherical Coordinates)

点 $P$ 的球坐标 $(\rho, \theta, \phi)$ 如下图所示：

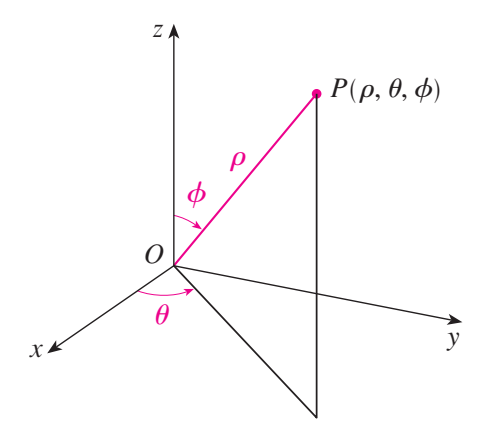
其中 $\rho = |OP|$ 为 $P$ 与原点的距离， $\theta$ 的定义和圆柱坐标的一样， $\phi$ 是 $z$ 轴正方向与线段 $OP$ 的夹角。注意到：
$\rho\ge 0\qquad 0\le\phi\le\pi$
球坐标在具有关于点对称的性质问题上较为常用，其中原点被设为该点。
从下图中可以看出直角坐标与球坐标的关系：

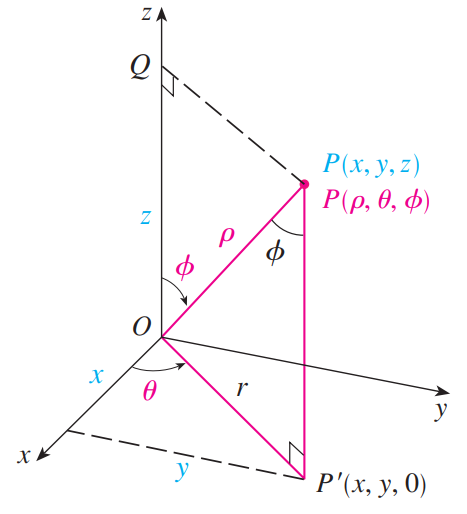
从三角形 $OPQ$ 和 $OPP’$ 中可以得出：
$z = \rho\cos\phi\qquad r = \rho\sin\phi$
而 $x = r\cos\theta$ ， $y = r\sin\theta$ ，所以将球坐标转化为直角坐标的公式为：
$x = \rho\sin\phi\cos\theta\qquad y = \rho\sin\phi\sin\theta\qquad z = \rho\cos\phi \tag{8.1}$
此外，距离公式表明：
$\rho^2 = x^2 + y^2 + z^2 \tag{8.2}\label{距离公式}$
公式 $\eqref{距离公式}$ 可以用来将直角坐标转化为球坐标。

用球坐标来求三重积分

在球坐标系中，长方体的对应图形为球楔(spherical wedge)：
$E = \{ (\rho, \theta, \phi)\ |\ a\le\rho\le b,\ \alpha\le\theta\le \beta,\ c\le\phi\le d \}$
其中 $a\ge 0$ 且 $\beta - \alpha\le 2\pi$ ，$d - c\le 2\pi$ 。
用等间距的球面 $\rho = \rho_i$ 、半平面 $\theta = \theta_j$ 和半圆锥 $\phi = \phi_k$ 将 $E$ 分割成更小的球楔 $E_{ijk}$ ，如下图所示：
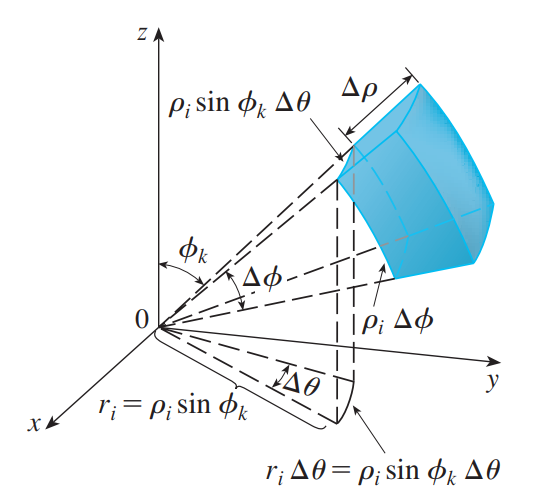
上图同样说明 $E_{ijk}$ 可以近似为三边长分别为 $\Delta\rho$ ， $\rho_i\Delta\phi$ 和 $\rho_i\sin\phi_k\Delta\theta$ 的长方体，所以 $E_{ijk}$ 的体积可以近似为
$\Delta V_{ijk}\approx (\Delta\rho)(\rho_i\Delta\phi) (\rho_i\sin\phi_k\Delta\theta) = \rho_i^2\sin\phi_k \Delta\rho \Delta\theta \Delta\phi$
可以证明，在中值定理的帮助下， $E_{ijk}$ 的准确体积公式为
$\Delta V_{ijk} = \tilde\rho_i^2\sin\tilde\phi_k \Delta\rho \Delta\theta \Delta\phi$
其中 $(\tilde{\rho_i}, \tilde{\theta_i}, \tilde{\phi_i})$ 为 $E_{ijk}$ 中的某点。令 $(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)$ 为该点的直角坐标，则
$\begin{align} \iiint\limits_Ef(x, y, z)dV &= \lim_{l, m, n\to\infty} \sum_{i = 1}^l\sum_{j = 1}^m\sum_{k = 1}^n f(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\Delta V_{ijk} \\&= \lim_{l, m, n\to\infty} \sum_{i = 1}^l\sum_{j = 1}^m\sum_{k = 1}^n f( \tilde\rho_i\sin\tilde\phi_k\cos\tilde\theta_j, \tilde\rho_i\sin\tilde\phi_k\sin\tilde\theta_j, \tilde\rho_i\cos\tilde\phi_k ) \tilde\rho_i^2\sin\tilde\phi_k \Delta\rho \Delta\theta \Delta\phi \end{align}$
这个和即为函数
$F(\rho, \theta, \phi) = f( \rho\sin\phi\cos\theta, \rho\sin\phi\sin\theta, \rho\cos\phi ) \rho^2\sin\phi$
的黎曼和。
最终，我们得出球坐标的三重积分公式(formula for triple integration in spherical coordinates)：

其中 $E$ 是由

确定的球楔形积分区域。
- 公式 $\eqref{积分1}$ 的意思是，将一个三重积分用公式
  $x = \rho\sin\phi\cos\theta\qquad y = \rho\sin\phi\sin\theta\qquad z = \rho\cos\phi$
  从直角坐标转换成球坐标，相应改变积分界限，并将 $dV$ 替换成 $\rho^2\sin\phi\ d\rho\ d\theta\ d\phi$ 。
- 这个公式也可以扩展到更一般的球坐标区域，比如：
  $E = \{ (\rho, \theta, \phi)\ |\ \alpha\le\theta\le \beta,\ c\le\phi\le d,\ g_1(\theta, \phi)\le \rho\le g_2(\theta, \phi) \}.$