Calculus笔记-15.6-三重积分

2024-05-05

Calculus笔记-15.6-三重积分

三重积分

考虑特例：
- 三元函数 $f$ 被定义于长方体：
  $B = \{(x, y, z)\ |\ a\le x\le b,\ c\le y\le d,\ r\le z\le s\} \tag{6.1}$
- 首先将 $B$ 分解成子长方体。
  - 将区间 $[a, b]$ 分解成 $l$ 个长 $\Delta x$ 的子区间 $[x_{i - 1}, x_i]$
  - 将区间 $[c, d]$ 分解成 $m$ 个长 $\Delta y$ 的子区间 $[y_{j - 1}, y_j]$
  - 将区间 $[r, s]$ 分解成 $n$ 个长 $\Delta z$ 的子区间 $[z_{k - 1}, z_k]$
    
    穿过子区间端点，平行于坐标平面的平面将 $B$ 分解成 $lmn$ 个子长方体：
    $B_{ijk} = [x_{i - 1}, x_i]\times [y_{j - 1}, y_j]\times [z_{k - 1}, z_k]$
    
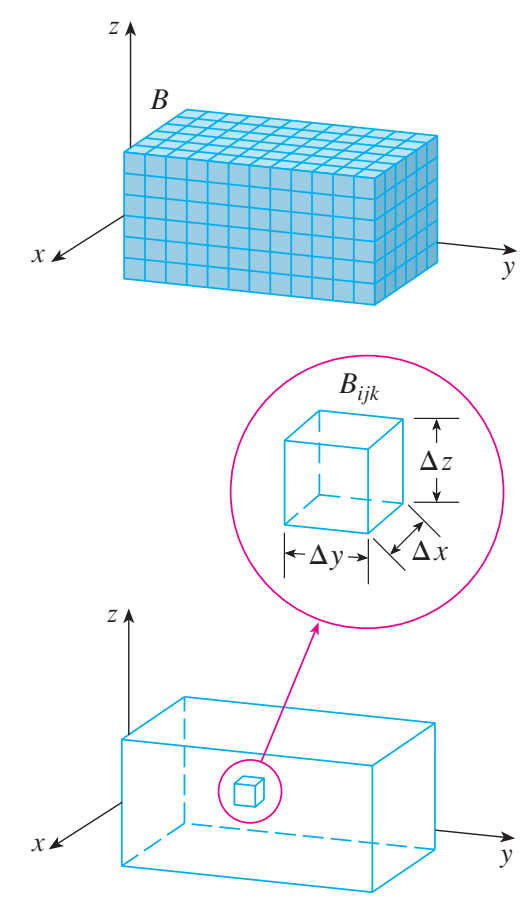
    如图所示，每一个子长方体面积都为 $\Delta V = \Delta x\Delta y\Delta z$ 。
- 则定义三重黎曼和：
  $\sum_{i = 1}^l\sum_{j = 1}^m\sum_{k = 1}^n f(x_{ijk}^*,y_{ijk}^*,z_{ijk}^*)\Delta V \tag{6.2}\label{三重黎曼和}$
  其中采样点 $(x_{ijk}^,y_{ijk}^,z_{ijk}^*)$ 位于 $B_{ijk}$ 内。
- 定义三重积分为 $\eqref{三重黎曼和}$ 的极限：
  - $f$ 在长方体 $B$ 区域内的三重积分为：
    $\iiint\limits_Bf(x, y, z)dV = \lim_{l, m, n\to\infty} \sum_{i = 1}^l \sum_{j = 1}^m \sum_{k = 1}^n f(x_{ijk}^*,y_{ijk}^*,z_{ijk}^*) \Delta V \tag{6.3}\label{三重积分1}$
    如果该极限存在。
  - 如果 $f$ 连续则其三重积分存在。
- 将采样点选为 $(x_i, y_j, z_k)$ ，则定义式看起来会比较简单：
  $\iiint\limits_Bf(x, y, z)dV = \lim_{l, m, n\to\infty} \sum_{i = 1}^l \sum_{j = 1}^m \sum_{k = 1}^n f(x_i,y_j,z_k) \Delta V \tag{6.4}\label{三重积分2}$
- 通过迭代积分来计算三重积分：
  - 如果 $f$ 在长方体 $B = [a, b]\times[c, d]\times[r, s]$ 内连续，则 $\iiint\limits_Bf(x, y, z)dV = \int_r^s\int_c^d\int_a^bf(x, y, z) dxdydz \tag{6.5}\label{三重积分3}$ Fubini定理对三重积分同样生效。
考虑对广义有界区域 $\mathbf{E}$ 的三重积分(triple integral over a general bounded region $\mathbf{E}$ )：
- 用长方体 $B$ 包围 $E$ ：
  $\iiint\limits_Ef(x, y, z)dV = \iiint\limits_BF(x, y, z)dV$
  其中 $F$ 满足在 $E$ 内时等于 $f$ ，在 $E$ 外时等于 $0$ 。该积分在 $f$ 连续且 $E$ “足够平滑(reasonably smooth)”时存在。
- 关注连续函数 $f$ 和一些特定的区域：
  - 如果 $E$ 被两个关于 $x$ 和 $y$ 的二元函数的图像所包围，即
    
    时，它被称为第一类积分区域，则
    - 若 $D$ 在 $xy$ 平面的投影是第一类积分区域，则式 $\eqref{第一类1}$ 变成：
      $\iiint\limits_Ef(x, y, z)dV = \int_b^a\int_{g_1(x)}^{g_2(x)} \int_{u_1(x, y)}^{u_2(x, y)}f(x, y, z)dzdydx \tag{6.8}\label{第一类2}$
    - 若 $D$ 在 $xy$ 平面的投影是第二类积分区域，则式 $\eqref{第一类1}$ 变成：
      $\iiint\limits_Ef(x, y, z)dV = \int_c^d\int_{h_1(y)}^{h_2(y)} \int_{u_1(x, y)}^{u_2(x, y)}f(x, y, z)dzdxdy \tag{6.9}\label{第一类3}$
  - 满足
    $E = \{(x, y, z)\ |\ (y, z)\in D,\ u_1(y, z)\le x\le u_2(y, z)\} \tag{6.10}$
    的区域 $E$ 被称为第二类积分区域，对 $E$ 的积分为：
    $\iiint\limits_Ef(x, y, z)dV = \iint\limits_D\left[\int_{u_1(y, z)}^{u_2(y, z)}f(x, y, z)dx\right]dA \tag{6.11}\label{第二类}$
  - 类似地，满足
    $E = \{(x, y, z)\ |\ (x, z)\in D,\ u_1(x, z)\le y\le u_2(x, z)\} \tag{6.12}$
    的区域 $E$ 被称为第三类积分区域，对 $E$ 的积分为：
    $\iiint\limits_Ef(x, y, z)dV = \iint\limits_D\left[\int_{u_1(x, z)}^{u_2(x, z)}f(x, y, z)dy\right]dA \tag{6.13}\label{第三类}$

三重积分的应用

如果 $f(x, y, z)\ge 0$ ，则三重积分 $\iiint_Ef(x, y, z)dV$ 代表四维空间中的“超体积”。
若对于 $E$ 上的所有点， $f(x, y, z) = 1$ ，则三重积分表示 $E$ 的体积：
$V(E) = \iiint\limits_Ef(x, y, z)dV \tag{6.14}\label{体积}$
若占据区域 $E$ 的物体的密度函数为 $\rho(x, y, z)$ ，则对于任意点 $(x, y, z)$ ，其质量为
$m = \iiint\limits_E\rho(x, y, z)dV \tag{6.15}\label{质量}$
其关于三个坐标平面的力矩分别为
$M_{yz} = \iiint\limits_Ex\rho(x, y, z)dV \tag{6.16}\label{力矩1}$ $M_{xz} = \iiint\limits_Ey\rho(x, y, z)dV \tag{6.17}\label{力矩2}$ $M_{xy} = \iiint\limits_Ez\rho(x, y, z)dV \tag{6.18}\label{力矩3}$
其质心位于点 $(\bar{x}, \bar{y}, \bar{z})$ ，其中
$\bar{x} = \frac{M_{yz}}m\qquad \bar{y} = \frac{M_{xz}}m\qquad \bar{z} = \frac{M_{xy}}m \tag{6.19}\label{重心}$
若物体的密度是常数，则其质心被称为 $E$ 的形心(centroid)。
物体关于三个坐标轴的转动惯量分别为
$I_x = \iiint\limits_E(y^2 + z^2)\rho(x, y, z)dV \tag{6.20}\label{转动惯量1}$ $I_y = \iiint\limits_E(x^2 + z^2)\rho(x, y, z)dV \tag{6.21}\label{转动惯量2}$ $I_z = \iiint\limits_E(x^2 + y^2)\rho(x, y, z)dV \tag{6.22}\label{转动惯量3}$
占据区域 $E$ ，电荷密度为 $\sigma(x, y, z)$ 的物体的总电荷量(electric charge)为
$Q = \iiint\limits_E\sigma(x, y, z)dV \tag{6.23}\label{电荷量}$
对于三个连续随机变量 $X$ 、 $Y$ 和 $Z$ ，其联合分布函数(joint density function是一个满足 $(X, Y, Z)$ 位于 $E$ 的概率为

的函数 $f$ 。
- 特别地，
  $P(a\le X\le b,\ c\le Y\le d,\ r\le Z\le s) = \int_a^b\int_c^d\int_r^sf(x, y, z)dzdydx \tag{6.25}\label{联合分布函数2}$
- 联合分布函数满足如下性质：
  - $f(x, y, z)\ge 0$
  - $\int_{-\infty}^\infty\int_{-\infty}^\infty\int_{-\infty}^\infty f(x, y, z)dzdydx = 1$