Calculus笔记-15.5-曲面面积

Calculus笔记-15.5-曲面面积

• 令 $S$ 为方程 $z = f(x, y)$ 所确定的方程，其中 $f$ 具有连续偏导数，且 $f(x, y)\ge 0$ ，其定义域为 $D$ 。将 $D$ 分割成小矩形 $R_{ij}$ ，其面积为 $\Delta A = \Delta x\Delta y$ 。若 $(x_i, y_j)$ 是 $R_{ij}$ 最接近原点的一角，令 $P_{ij}(x_i, y_j, f(x_i, y_j))$ 为其正上方位于 $S$ 内的点（如下图），

  

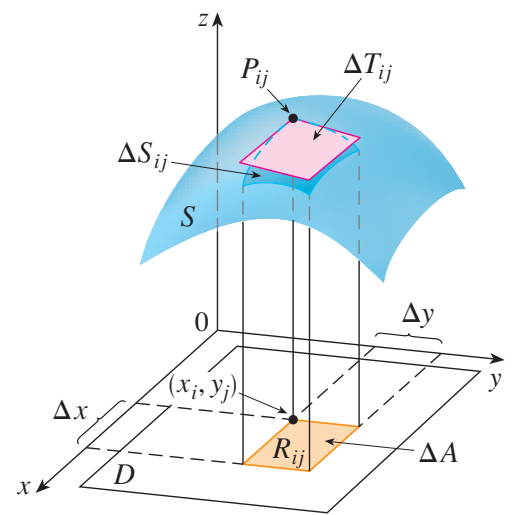
  则

  • $S$ 过 $P_{ij}$ 点的切平面是在 $P_{ij}$ 点附近对于 $S$ 的一个近似；
  • 切平面这一部分的面积 $\Delta T_{ij}$ 就是对于 $\Delta S_{ij}$ 的一个近似；
  • 总和 $\sum\sum\Delta T_{ij}$ 就是对 $S$ 的总面积的一个近似;

  • 且矩形数量越多，近似效果越好。

    则可以定义 $S$ 的曲面面积(surface area)为

    $$A(S) = \lim_{m, n\to\infty} \sum_{i = 1}^m\sum_{j = 1}^n \Delta T_{ij} \tag{5.1}\label{曲面面积1}$$

• 为了寻找比式 $\eqref{曲面面积1}$ 更方便使用的公式，（如下图）令 $\mathbf{a}$ 和 $\mathbf{b}$ 为从 $P_{ij}$ 出发，沿着面积为 $\Delta T_{ij}$ 的平行四边形的两边前进的向量

  

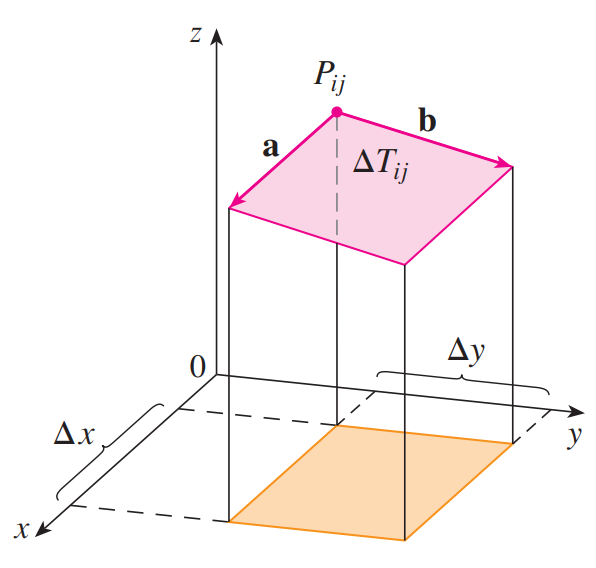
  • 则 $\Delta T_{ij} = |\mathbf{a}\times\mathbf{b}|$

  • 则

    $$\mathbf{a} = \Delta x\mathbf{i}\ +\ f_x(x_i, y_j)\Delta x\mathbf{k}\\ \mathbf{b} = \Delta x\mathbf{j}\ +\ f_y(x_i, y_j)\Delta y\mathbf{k}$$

  • 而

    $$\begin{align} \mathbf{a}\times\mathbf{b} &= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ \Delta x & 0 & f_x(x_i, y_j)\Delta x\\ 0 &\Delta y & f_y(x_i, y_j)\Delta y\\ \end{vmatrix} \\&= [-f_x(x_i, y_j)\mathbf{i}\ -\ f_y(x_i, y_j)\mathbf{j}\ +\ \mathbf{k}] \Delta A \end{align}$$

  • 因此

    $$\Delta T_{ij} = |\mathbf{a}\times\mathbf{b}| = \sqrt{[f_x(x_i, y_j)]^2\ +\ [f_x(x_i, y_j)]^2\ +\ 1} \Delta A$$

  • 由定义 $\eqref{曲面面积1}$ 可知

    $$\begin{align} A(S) &= \lim_{m, n\to\infty} \sum_{i = 1}^m\sum_{j = 1}^n \Delta T_{ij} \\&= \lim_{m, n\to\infty} \sum_{i = 1}^m\sum_{j = 1}^n \sqrt{[f_x(x_i, y_j)]^2\ +\ [f_x(x_i, y_j)]^2\ +\ 1} \Delta A \end{align}$$

  • 由二重积分的定义，我们有：

    • 由方程 $z = f(x, y), (x, y)\in D$ ，其中 $f_x$ 和 $f_y$ 为连续函数确定的曲面面积为： $$A(S) = \iint\limits_D \sqrt{[f_x(x_i, y_j)]^2\ +\ [f_x(x_i, y_j)]^2\ +\ 1} \Delta A \tag{5.2}\label{曲面面积2}$$ 也可写作 $$A(S) = \iint\limits_D \sqrt{(\frac{\partial z}{\partial x})^2\ +\ (\frac{\partial z}{\partial y})^2\ +\ 1} \Delta A. \tag{5.3}\label{曲面面积3}$$