Calculus笔记-9.6-捕食-被捕食者系统

9.6 捕食-被捕食者系统(Predator-Prey Systems)

定义

我们研究两个数量互相关联的物种, 捕食者与被捕食者的数量与时间 $t$ 的关系, 并定义被捕食者的数量为 $R(t)$ , 捕食者的数量为 $W(t)$ .

在一开始, 我们假设两个物种的数量之间没有关联.

对于被捕食者的数量, 我们设其自然增长率为 $k$ , 其中 $k$ 为正数, 则

$$\frac{dR}{dt} = kR$$

对于捕食者的数量, 我们设其净死亡率为 $r$ , 其中 $r$ 为正数, 则

$$\frac{dW}{dt} = -rW$$

---

现在我们认为捕食者与被捕食者的数量相关, 并且两者相遇的概率与两者的数量之积 $RW$ 正相关.

我们设两者相遇的概率对于被捕食者的减少影响因子为 $a$ , 对于捕食者的增长影响因子为 $b$ , 则有

$$\frac{dR}{dt} = kR - aRW\qquad\frac{dW}{dt} = -rW + bRW$$

式 $(89)$ 被称为捕食-被捕食者方程或Lotka-Volterra方程.

虽然一般来说很难找到 $R$ 和 $W$ 关于时间 $t$ 的显式方程, 但我们仍能通过方向场来估算其结果, 或通过计算机来画出 $R-W$ 图像.

我们把 $R-W$ 平面中表示平衡解的点称为平衡点.

我们把 $R-W$ 平面称为相平面(phase plane), 把解的曲线称为相轨迹(phase trajectories), 把包含平衡点和典型相轨迹的平面称作相图(phase portrait).

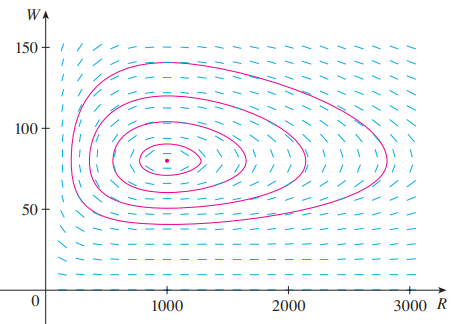
相图

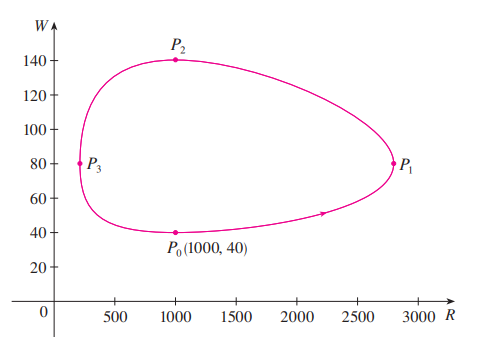
相轨迹