Calculus笔记-9.2-方向场与欧拉方程

9.2 方向场与欧拉方程(Direction Fields and Euler’s Method)

方向场

当我们试图解出下列初值问题

$$y' = x + y\qquad y(0) = 1$$

时, 我们不知道解的公式, 但可以通过代入 $x$ , $y$ 的值, 得到下列图表:

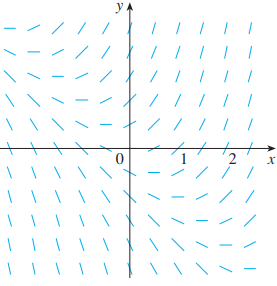
这个图表被称为方向场， 它描述了在一定 $x$ , $y$ 的离散值下所求函数的方向情况, 借此我们可以大概画出经过所求点的函数图像:

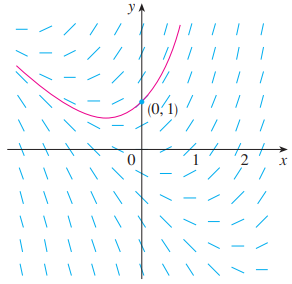
(上图为经过点 $(0, 1)$ 的函数图像)

---

一般来说, 当我们有下列形式的一阶微分方程

$$y' = F(x,\ y)$$

时, 因为上式表示了函数 $f$ 在点 $(x,\ y)$ 的斜率, 故我们可以在一些点 $(x,\ y)$ 处画出斜率为 $F(x, y)$ 的线段, 这样的结果被称为方向场.

欧拉法

解一阶微分方程的初值问题时, 我们有如下方法来估计所求函数的图像:

设 $y’ = F(x,\ y)$ , $y(x_0) = y_0$ , 同时我们有步长 $h$ , 在点 $x_n = x_{n - 1} + h$ , 则解的估计值为

$$y_n = y_{n - 1} + hF(x_{n - 1},\ y_{n - 1})\qquad n = 1,\ 2,\ 3,\ \dots$$

该法被称为欧拉法.