Calculus笔记-5.4-功

5.4 功(Work)

根据牛顿第二定律, 我们有

$$F = ma = m\frac{d^2s}{dt^2}$$

根据功的定义, 我们有

$$W = Fd$$

如果 $F$ 是一个随时间变化的量, 则我们可以将单位时间内对物体做的功 $W_i$ 用采样点的力 $F(x^*_i)$ 和位移 $\Delta x$ 来表示, 即

$$W_i\approx f(x^*_i)\Delta x$$

则我们可以用黎曼和来近似表示总功 $W$ :

$$W\approx\sum^n_{i = 1}f(x^*_i)\Delta x$$

当 $n\to \infty$ 时, 这个近似和会变得越来越精确, 因此我们定义物体从 $a$ 运动到 $b$ 所做的功为该近似值在 $n\to\infty$ 下的极限, 即

$$W = \lim_{n\to\infty}\sum^n_{i = 1}f(x^*_i)\Delta x = \int^b_af(x)dx$$

例题: 对弹簧做的功

问题

将一个弹簧从原长10cm拉到15cm长需要的力为40N, 那么将其从15cm长拉到18cm长需要做多少功?

解

根据胡克定律, 我们有

$$f(x) = kx$$

代入原条件, 我们有

$$0.05k = 40\qquad k = \frac{40}{0.05} = 800$$

则求出 $f(x) = 800x$ , 则将弹簧从15cm长拉到18cm长所需做功则为

$$\begin{align*} W &= \int^{0.08}_{0.05}800xdx = 800[\frac{x^2}{2}]^{0.08}_{0.05}\\ &= 400[(0.08)^2 - (0.05)^2] = 1.56J \end{align*}$$

例题: 对非质点物体做的功

问题

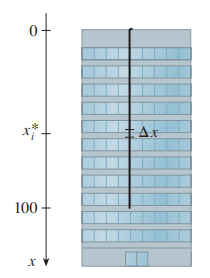
如图, 一根重200磅, 长100英尺的电线在楼顶垂直挂着. 要想把整根电线拉倒楼顶, 需要做多少功?

解

磅是重量单位, 因此我们不需要计算力 $F$ . 若我们将电线分为 $n$ 个小条并认为对其各部分做功一致, 则第 $i$ 根电线重 $(2\ lb/ft)(\Delta x\ ft) = 2\Delta x\ lb$ , 则对其做功为

$$(2\Delta x)\cdot x^*_i = 2x^*_i\Delta x$$

则总做功为

$$W = \lim_{n\to\infty}\sum^n_{i = 1}2x^*_i\Delta x = \int^{100}_{0}2xdx$$