Calculus笔记-5.3-旋转壳的体积

2024-05-04

5.3 旋转壳的体积(Volumes by Cylindrical Shells)

问题引入

求由区间 $y = 2x^2 - x^3$ 和 $y = 0$ 围成, 绕 $y$ 轴旋转得到的物体的体积

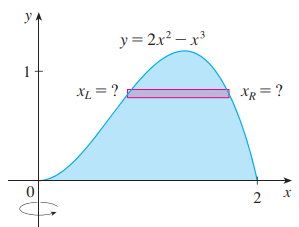
我们考察这样一个近似矩形, 试图用垫圈法来解决, 却发现矩形的左、右坐标 $x_L$ 和 $x_R$ 难以取得.

为解决这类问题, 我们引入一个新的模型:

圆柱壳法

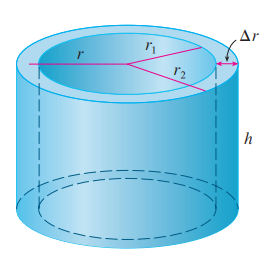
如图, 我们以一个圆柱壳来近似看待所求区间的体积, 则其体积:

$\begin{align*} V &= V_2 - V_1\\ &= \pi r^2_2h - \pi r^2_1h = \pi (r^2_2 - r^2_1)h\\ &= \pi (r_2 + r_1)(r_2 - r_1)h\\ &= 2\pi\frac{r_2 + r_1}{2}h(r_2 - r_1) \end{align*}$

令 $\Delta r = r_2 - r_1$ (圆柱壳的厚度), 令 $r = \frac{1}{2}(r_2 + r_1)$ (圆柱壳的平均半径), 则式 $(10)$ 能写成

$V = 2\pi rh\Delta r$

式 $(11)$ 可以如下方法记忆:

$V = [\text{周长}][\text{高度}][\text{厚度}]$

我们可用该法来估计如下物体的体积

一般物体的体积

问题:

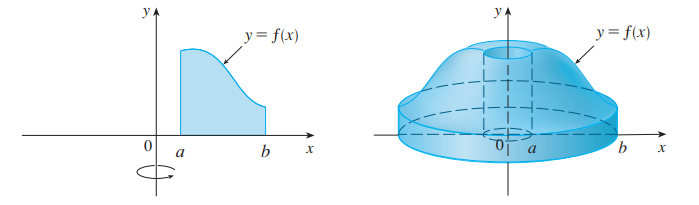
求图中由 $y = f(x)$ (假设 $f(x)\geq0$ ), $y = 0$ , $x = a$ , $x = b$ ( $b > a \geq 0$ )围成的图形绕 $y$ 轴旋转得到的物体的体积

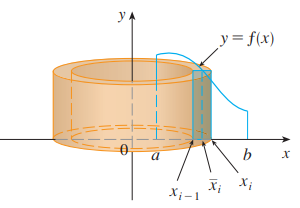
如图, 我们将区间 $[a,\ b]$ 分成 $n$ 个子区间 $[x_{i - 1},\ x_i]$ , 考察单个区间内圆柱壳的体积, 可得:

$V_i = (2\pi\bar{x})[f(\bar{x_i})]\Delta x$

我们可估计物体的体积:

$V \approx \sum^n_{i = 1}V_i = \sum^n_{i = 1}2\pi \bar{x_i}f(\bar{x_i})\Delta x$

随着 $n\to\infty$ , 该估计变得越来越准确.

由积分的定义, 我们可以得到:

$\lim_{n\to\infty} \sum^n_{i = 1}2\pi \bar{x_i}f(\bar{x_i})\Delta x = \int^b_a2\pi xf(x)dx$

因此有如下定义:

定义

样例中从 $a$ 到 $b$ , 由曲线 $y = f(x)$ 绕 $y$ 轴旋转围成的物体的体积, 等于

$V = \int^b_a2\pi xf(x)dx\qquad \text{其中}0\leq a < b.$

证明

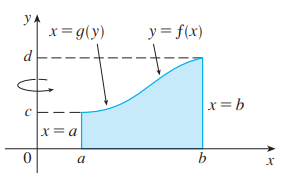
我们设旋转体如上图, 则旋转体的体积为

$V = \pi bd - \pi ad - \int^d_c\pi [g(y)]^2dy$

通过下列步骤, 式 $(21)$ 可化为

$\begin{align} V &= \pi b^2d - \pi a^2c - \pi\int^d_c[g(f(x))]^2d(f(x))\notag\\ &= \pi b^2d - \pi a^2c - \pi\int^b_ax^2f'(x)dx\notag\\ &= \pi b^2d - \pi a^2c - \pi\left\{[x^2f(x)]^b_a - \int^b_a2xf(x)dx\right\}\notag\\ &= \pi b^2d - \pi a^2c - \pi\left\{b^2d + a^2c - \int^b_a2xf(x)dx\right\}\notag\\ &= \int^b_a2\pi xf(x)dx \end{align}$

式 $(20)$ 成立, 证毕.

盘片法、垫圈法和圆柱壳法的比较

何时采用盘片/垫圈法, 何时采用圆柱壳法?

我们考察三个典型物体:

求正截面为半径为1的半圆,侧截面为高为y的等边三角形所围成物体的体积

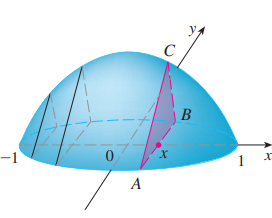
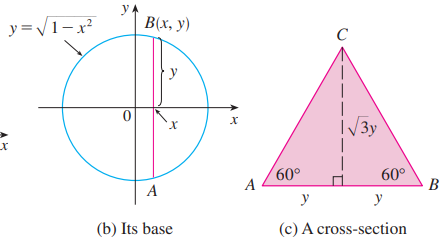
如图(b)与图(c), 我们考察其正截面与侧截面, 采用盘片法求得其体积;

求曲线 $y = x$ 和 $y = x^2$ 所围成图形绕直线 $x = -1$ 所围成物体的体积

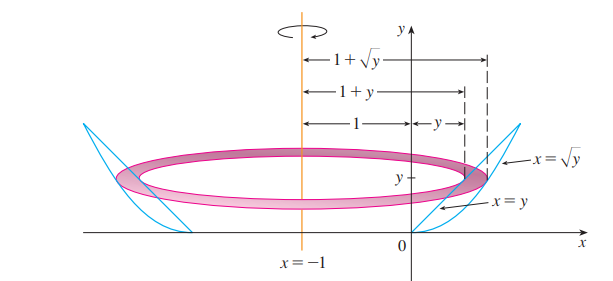
如图, 我们考察其横截面, 采用垫圈法求得其体积;

求曲线 $y = x - x^2$ 和 $y = 0$ 所围成图形绕直线 $x = 2$ 所围成物体的体积

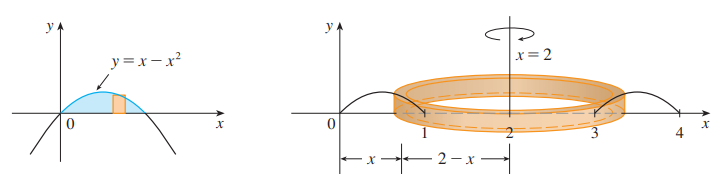
如图, 我们考察其横截面, 采用圆柱壳法求得其体积.

结论:

对于一般物体的体积, 我们都首先考察其横截面, 画出估计矩形, 再采用合适的模型进行求解.

对于实心物体的体积, 我们采用盘片法进行求解;
对于空心物体的体积, 我们采用垫圈法或圆柱壳法求得其体积.

垫圈法与圆柱壳法的不同:
- 如果估计矩形的左、右端点坐标较容易写出表达式, 我们采用垫圈法;
- 如果估计矩形的高较容易写出表达式, 则我们采用圆柱壳法.

主要观点:

求物体的体积, 我们用矩形去逼近其截面面积, 用 $x$ 或 $y$ 的变化量去表示矩形面积中不易表示的量, 用x或y的对应表达式去表示矩形面积中较易表示的量, 从而达到化简问题的目的.