Calculus笔记-15.4-二重积分的应用

2024-05-04

Calculus笔记-15.4-二重积分的应用

密度和质量

如图，考虑一片具有变化密度的叶子：

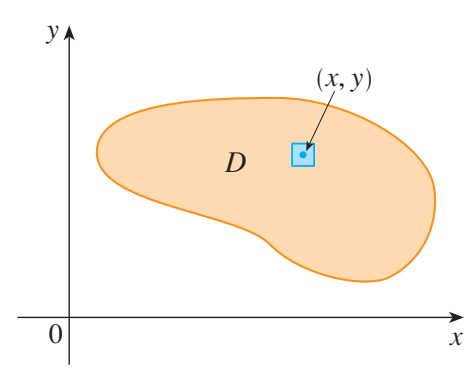
设叶片占据区域 $xy$ 平面内的区域 $D$ ，其在 $D$ 内点 $(x, y)$ 的密度为 $\rho(x, y)$ ，其中 $\rho$ 是在 $D$ 上的连续函数。这意味着：
$\rho(x, y) = \lim\frac{\Delta m}{\Delta A}$
其中 $\Delta m$ 和 $\Delta A$ 分别为包含点 $(x, y)$ 的小矩形的质量和面积，而极限在矩形的大小趋于 $0$ 时取得。
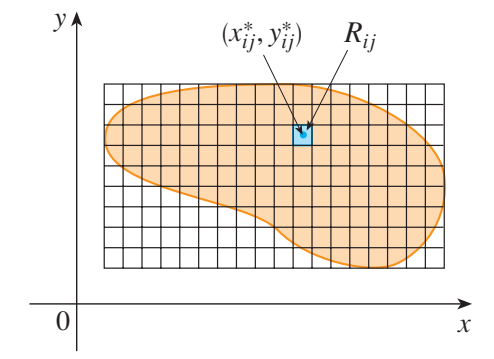
如上图，为了寻找叶片的总质量 $m$ ，我们将包含 $D$ 的矩形区域 $R$ 分割成同样大小的子矩形 $R_{ij}$ ，并设区域 $D$ 外的 $\rho(x, y) = 0$ 。如果在 $R_{ij}$ 内选择采样点 $(x_{ij}^*, y_{ij}^*)$ ，则占据 $R_{ij}$ 的叶片的质量近似于 $\rho(x_{ij}^*, y_{ij}^*)\Delta A$ ，其中 $\Delta A$ 为 $R_{ij}$ 的面积。
将质量相加，我们能够得到对于总质量的一个近似：
$m\approx \sum_{i = 1}^k\sum_{j = 1}^l \rho(x_{ij}^*, y_{ij}^*)\Delta A$
通过增加子矩形的数量，我们得到了这个近似的极限，从而能够计算出叶片的总质量 $m$ ：
$m = \lim_{k, l\to\infty} \sum_{i = 1}^k\sum_{j = 1}^l \rho(x_{ij}^*, y_{ij}^*)\Delta A = \iint\limits_D\rho(x, y)dA \tag{4.1}\label{质量公式}$
这个“密度”的范围也可以扩展到它的其他物理含义，比如：
- 设一个占据范围 $D$ 的电容器在 $D$ 内点 $(x, y)$ 的电容密度为 $\sigma(x, y)$ ，则其总电量 $Q$ 为： $Q = \iint\limits_D\sigma(x, y)dA \tag{4.2}\label{电量公式}$

力矩(moments)和质心(centers of mass)

力矩

设叶片占据区域 $D$ ，且有密度函数 $\rho(x, y)$ ，其关于单个坐标轴的力矩为其质量和与轴的有向距离的乘积。
将 $D$ 分成小矩形，单个矩形 $R_{ij}$ 的质量估计值为 $\rho(x_{ij}^*, y_{ij}^*)\Delta A$ ，则我们可以估计 $R_{ij}$ 关于 $x$ 轴的力矩为 $[\rho(x_{ij}^*, y_{ij}^*)\Delta A]y_{ij}^*$
将力矩相加并取极限，我们得到整个叶片关于 $x$ 轴的力矩： $M_x = \lim_{m, n\to\infty} \sum_{i = 1}^m\sum_{j = 1}^n y_{ij}^*\rho(x_{ij}^*, y_{ij}^*)\Delta A = \iint\limits_Dy\rho(x, y)dA \tag{4.3}\label{x轴力矩}$
相似地，我们可以得到叶片关于 $y$ 轴的力矩： $M_y = \lim_{m, n\to\infty} \sum_{i = 1}^m\sum_{j = 1}^n x_{ij}^*\rho(x_{ij}^*, y_{ij}^*)\Delta A = \iint\limits_Dx\rho(x, y)dA \tag{4.4}\label{y轴力矩}$

质心

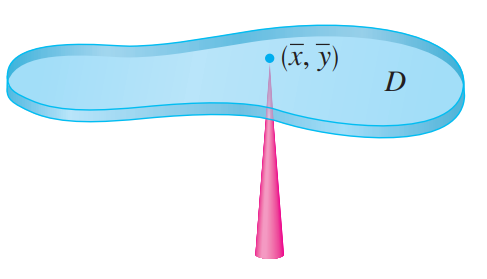
我们定义质心是满足 $m\bar{x} = M_y,\ m\bar{y} = M_x$ 的点 $(\bar{x}, \bar{y})$ ，其物理含义是质量分散在整个叶片之上的表现和整个叶片的质量集中在质心上时的表现相同（如下图）。
定义

占据区域 $D$ ，具有密度函数 $\rho(x, y)$ 的叶片的质心的坐标 $(\bar{x}, \bar{y})$ 为
$\bar{x} = \frac{M_y}m = \frac1m \iint\limits_Dx\rho(x, y)dA\qquad \bar{y} = \frac{M_x}m = \frac1m \iint\limits_Dy\rho(x, y)dA\qquad \tag{4.5}\label{重心公式}$
其中 $m$ 由
$m = \iint\limits_D\rho(x, y)dA\qquad$
确定。

转动惯量(moment of inertia)

质量为 $m$ 的粒子的转动惯量（也叫做二阶力矩）被定义为 $mr^2$ ，其中 $r$ 为粒子与轴的距离。我们将这个概念扩展到密度为 $\rho(x, y)$ ，占据空间 $D$ 的叶片。将 $D$ 分解为小矩形，估计每一个子矩形关于 $x$ 轴的转动惯量，并取极限和，得到的结果就是叶片关于 $x$ 轴的转动惯量：
$I_x = \lim_{m, n\to\infty} \sum_{i = 1}^m\sum_{j = 1}^n (y_{ij}^*)^2\rho(x_{ij}^*, y_{ij}^*)\Delta A = \iint\limits_Dy^2\rho(x, y)dA \tag{4.6}\label{x轴转动惯量}$
相似地，叶片关于 $y$ 轴的转动惯量为：
$I_y = \lim_{m, n\to\infty} \sum_{i = 1}^m\sum_{j = 1}^n (x_{ij}^*)^2\rho(x_{ij}^*, y_{ij}^*)\Delta A = \iint\limits_Dx^2\rho(x, y)dA \tag{4.7}\label{y轴转动惯量}$
叶片关于原点的转动惯量(moment of inertia about the origin)，也叫做极转动惯量(polar moment of inertia)，为：
$I_0 = \lim_{m, n\to\infty} \sum_{i = 1}^m\sum_{j = 1}^n [(x_{ij}^*)^2 + (y_{ij}^*)^2] \rho(x_{ij}^*, y_{ij}^*)\Delta A = \iint\limits_D(x^2 + y^2)\rho(x, y)dA \tag{4.8}\label{极转动惯量}$
从式 $\eqref{极转动惯量}$ 可以得出 $I_0 = I_x + I_y$ 。
转动惯量在物理上表示物体在转动时的惯性。

回转半径(radius of gyration)

叶片关于某一轴的回转半径 $R$ 由公式
$mR^2 = I \tag{4.9}\label{回转半径}$
定义。其中 $m$ 是叶片的质量， $I$ 是叶片关于该轴的转动惯量。式 $\eqref{回转半径}$ 意味着当叶片的质量集中在轴距为 $R$ 的一点时其转动惯量与整个叶片的转动惯量相同。
特别地，我们可以给出叶片关于 $x$ 轴和 $y$ 轴的回转半径 $\bar{\bar{y}}$ 和 $\bar{\bar{x}}$ ：
$m\bar{\bar{y}}^2 = I_x \tag{4.10}\label{x轴回转半径}$ $m\bar{\bar{x}}^2 = I_y \tag{4.11}\label{y轴回转半径}$
当叶片的质量集中于点 $(\bar{\bar{x}}, \bar{\bar{y}})$ 时，它的转动惯量不会改变。

概率(Probability)

连续随机变量 $X$ 的概率密度函数(probability density function) $f$ 满足：
- $f(x)\ge 0$
- $\int_{-\infty}^{\infty}f(x)dx = 1$
  
  ，而 $X$ 落在区间 $[a, b]$ 内的概率为
  $P(a\le X\le b) = \int_a^bf(x)dx. \tag{4.12}\label{一元概率分布}$
考虑两个连续变量 $X$ 和 $Y$ ，它们的联合分布函数(joint density function)是一个满足 $(X, Y)$ 落在区域 $D$ 的概率为：
$p((X, Y)\in D) = \iint\limits_Df(x, y)dA \tag{4.13}\label{二元概率分布}$
的二元函数 $f$ 。
特别地，如果 $D$ 是一个矩形区域，则 $X$ 落在区间 $[a, b]$ 且 $Y$ 落在区间 $[c, d]$ 内的概率为：
$P(a\le X\le b,\ c\le X\le d) = \int_a^b\int_c^df(x, y)dydx \tag{4.14}\label{矩形区域概率分布}$
如下图所示。
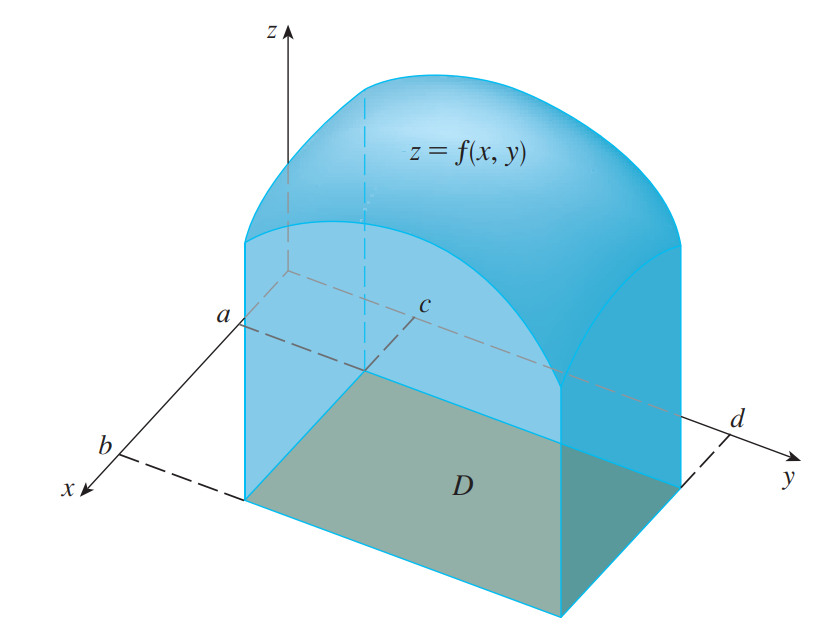
因为概率不可能为负数，且用区间 $[0, 1]$ 来衡量，所以联合分布函数满足如下性质：
- $f(x, y)\ge 0$
- $\iint\limits_{\mathbb{R}^2}f(x, y)dA = 1.$
  
  其中，对于 $\mathbb{R}^2$ 的二重积分被定义为对无限扩展的圆形或矩形区域取极限而得到的积分值。它是一个瑕积分，可以写成如下形式：
  $\iint\limits_{\mathbb{R}^2}f(x, y)dA = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(x, y)dxdy = 1 \tag{4.15}\label{二维空间概率分布}$
如果随机变量 $X$ 、 $Y$ 分别具有概率密度函数 $f_1(x)$ 和 $f_2(y)$ ，则当 $X$ 和 $Y$ 满足
$f(x, y) = f_1(x)f_2(y) \tag{4.16}\label{独立变量概率分布}$
时，它们被称为独立随机变量(independent random variables)。

期望(Expected Values)

当一元随机变量 $X$ 的概率密度函数为 $f$ 时，它的均值(mean)为：
$\mu = \int_{-\infty}^{\infty}xf(x)dx \tag{4.17}\label{一元随机变量均值}$
当二元随机变量 $X$ 和 $Y$ 满足联合分布函数 $f$ 时，我们分别定义其$X$均值($X$-mean) 和$Y$均值($Y$-mean)（也被称为 $X$ 和 $Y$ 的期望(expected values)）为
$\mu_1 = \iint\limits_{\mathbb{R}^2}xf(x, y)dA\quad 和 \quad \mu_2 = \iint\limits_{\mathbb{R}^2}yf(x, y)dA$
当单个随机变量的概率分布函数满足
$f(x) = \frac1{\sigma\sqrt{2\pi}}e^ {-(x - \mu)^2 / (2\sigma^2)}$
时，该变量满足正态分布，其中 $\mu$ 为均值， $\sigma$ 为标准差(standard deviation)。