Calculus笔记-15.3-极坐标的二重积分

Calculus笔记-15.3-极坐标的二重积分

极坐标二重积分的定义

• 有些时候，运用极坐标进行运算会更为方便：

  

• 

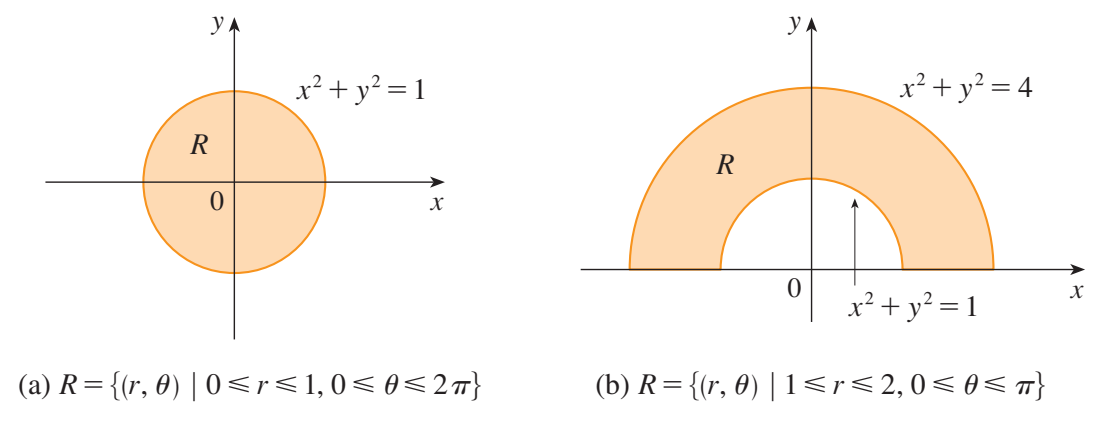
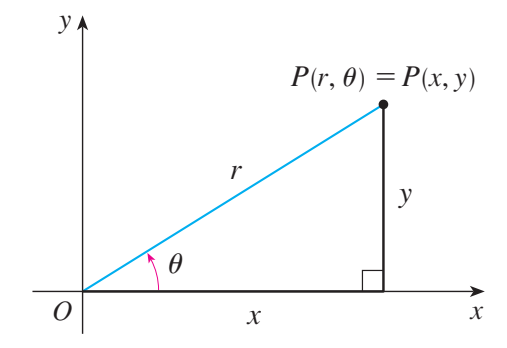
  回忆极坐标与直角坐标的关系：

  $$r^2 = x^2 + y^2\qquad x = r\cos\theta\qquad y = r\sin\theta$$

• 

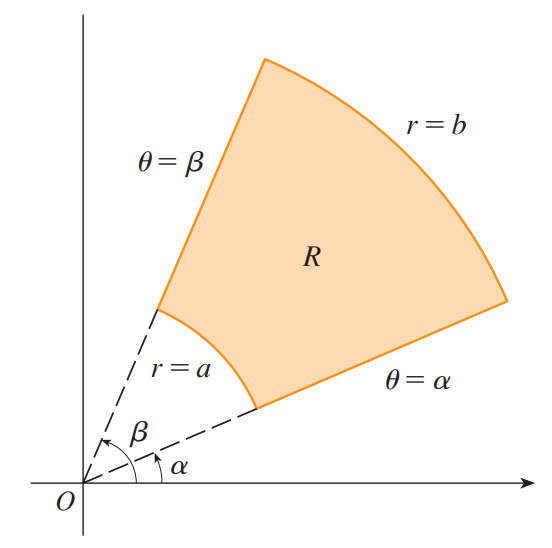
  上图中的面积是极矩形的一个特例：

  $$R = \{(r, \theta)\ |\ a\le r\le b, \alpha\le\theta\le\beta\}$$

• 为了计算二重积分 $\iint\limits_Rf(x, y)dA$ ，其中 $R$ 是一个极矩形

  • 我们将区间 $[a, b]$ 分割成 $m$ 个子区间 $[r_{i - 1}, r_i]$ ，每一个长 $\Delta r = (b - a) / m$

  • 将区间 $[\alpha, \beta]$ 分割成 $n$ 个子区间 $[\theta_{i - 1}, \theta_i]$ ，每一个长 $\Delta \theta = (\beta - \alpha) / n$

  • 则我们可以用圆弧 $r = r_i$ 和射线 $\theta = \theta_j$ 将极矩形 $R$ 分割成子极矩形 $R_{ij}$ （如下图）。

    

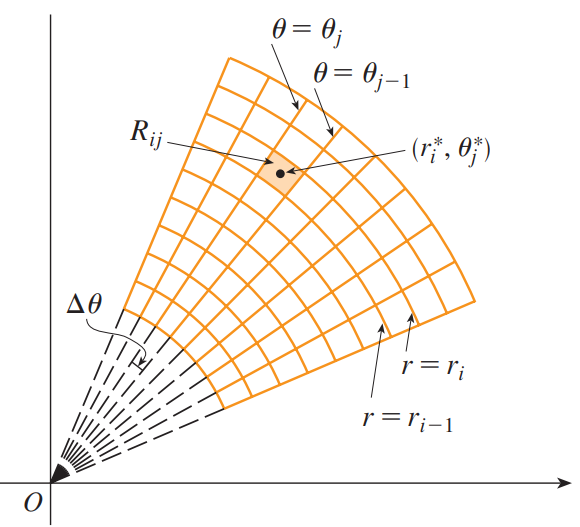
    其中

    • 极矩形的“中心” $$R_{ij} = \{(r, \theta)\ |\ r_{i - 1}\le r\le r_i, \theta_{i - 1}\le\theta\le\theta_i\}$$ 有极坐标 $$r_i^* = \frac12(r_{i - 1} + r_i)\qquad \theta_j^* = \frac12(\theta_{i - 1} + \theta_i)$$

  • 我们知道，半径 $r$ ，中心角为 $\theta$ 为扇形面积为

    $$\frac12r^2\theta \tag{3.1}\label{扇形面积}$$

  • 将两个中心角同为 $\Delta\theta = \theta_j - \theta_{j - 1}$ 的扇形面积相减，我们得到 $R_{ij}$ 的面积为：

    $$\begin{align} \Delta A_i &= \frac12r_i^2\Delta\theta - \frac12r_{i - 1}^2\Delta\theta\\ &= \frac12(r_i - r_{i - 1})(r_i + r_{i - 1}) \theta\\ &= r_i^*\Delta r\Delta\theta \end{align}$$

  • 虽然我们对于二重积分 $\iint_Rf(x, y)$ 的定义是关于矩形的，但（可以证明）对于连续的函数 $f$ ，使用极矩形也可以得到同样的结果。 $R_{ij}$ 中心的直角坐标为 $(r_i^*\cos\theta_j^*, r_i^*\sin\theta_j^*)$ ，则它的黎曼和可以表示为

    $$\sum_{i = 1}^m\sum_{j = 1}^n f(r_i^*\cos\theta_j^*, r_i^*\sin\theta_j^*) \Delta A_i = \sum_{i = 1}^m\sum_{j = 1}^n f(r_i^*\cos\theta_j^*, r_i^*\sin\theta_j^*) r_i^*\Delta r\Delta\theta \tag{3.2}\label{黎曼和1}$$

  • 如果令 $g(r, \theta) = rf(r\cos\theta, r\sin\theta)$ ，则式 $\eqref{黎曼和1}$ 可以写为

    $$\sum_{i = 1}^m\sum_{j = 1}^n g(r_i^*, \theta_j^*) \Delta r\Delta\theta \tag{3.3}\label{黎曼和2}$$

    也就是二重积分

    $$\int_\alpha^\beta \int_a^b g(r, \theta)drd\theta \tag{3.4}\label{积分1}$$

    的黎曼和

  • 因此我们有

    $$\begin{align} \iint\limits_Rf(x, y)dA &= \int_\alpha^\beta \int_a^b g(r, \theta)drd\theta\\ &= \int_\alpha^\beta \int_a^b f(r\cos\theta, r\sin\theta)rdrd\theta \end{align}$$

• 总结

  如果 $f$ 在极矩形 $R = \{(r, \theta)\ |\ a\le r\le b, \alpha\le\theta\le\beta\}$ 的范围内连续，其中 $0\le\beta - \alpha\le 2\pi$ ，则

  $$\iint\limits_Rf(x, y)dA = \int_\alpha^\beta \int_a^b f(r\cos\theta, r\sin\theta)rdrd\theta. \tag{3.5}\label{极坐标二重积分}$$

第一类极坐标二重积分

• 如果 $f$ 在极矩形 $R = \{(r, \theta)\ |\ \alpha\le\theta\le\beta,\ h_1(\theta)\le r\le h_2(\theta)\}$ 的范围内连续，则

  $$\iint\limits_Rf(x, y)dA = \int_\alpha^\beta \int_{h_1(\theta)}^{h_2(\theta)} f(r\cos\theta, r\sin\theta)rdrd\theta \tag{3.6}\label{第一类极坐标二重积分}$$

• 式 $\eqref{扇形面积}$ 其实是式 $\eqref{第一类极坐标二重积分}$ 的特例。