Calculus笔记-15.2-一般区域的二重积分

Calculus笔记-15.2-一般区域的二重积分

定义

• 为了对更广泛区域求得积分，我们假设 $D$ 是一个有界区域，并在 $R$ 内定义一个新函数 $F$ 满足

  $$F(x, y) = \begin{cases} f(x, y)& \qquad 如果(x, y)在D内\\ 0& \qquad 如果(x, y)在R内但不在D内 \end{cases} \tag{2.1}\label{F的定义}$$

• 如果 $F$ 在 $R$ 内可积分，则我们定义 $f$ 对 $D$ 的二重积分为

  $$\iint\limits_Df(x, y)dA = \iint\limits_RF(x, y)dA \qquad 其中F由式\eqref{F的定义}给出 \tag{2.2}\label{f的二重积分}$$

  $\eqref{f的二重积分}$ 具有意义，因为 $R$ 是一个矩形区域，因此 $\iint_RF(x, y)dA$ 之前就在15.1中被定义了。

• 当 $f(x, y)\ge 0$ 时，我们仍能将 $\iint_Df(x, y)dA$ 看作 $D$ 和 曲面 $z = f(x, y)$ 围成物体的体积（如下图）。

  

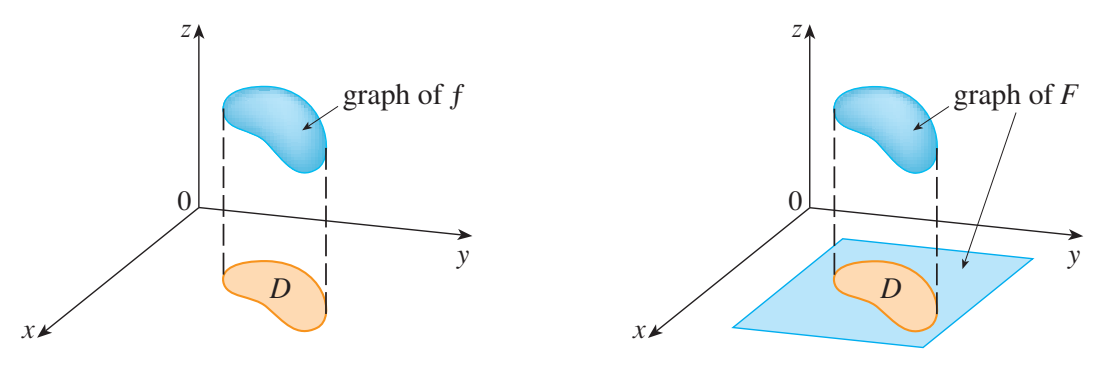
  上图同样说明 $F$ 可能在 $D$ 的边界点上不连续，但其在 $R$ 上的积分仍可能存在，只要满足 $f$ 在 $D$ 上连续而且 $D$ 的边界“表现良好”（这里不做讨论）即可。

两种积分类型

第一类二重积分

定义

若平面区域 $D$ 被两个关于 $x$ 的函数的图像所围成，即

$$D = \{(x, y)\ |\ a\le x\le b,\ g_1(x)\le y\le g_2(x)\}\\ (其中g_1和g_2在[a, b]内连续)$$

时，我们称其为第一类积分区域。

计算

为了计算第一类二重积分，我们选择包围 $D$ 的矩形区域 $R = [a, b]\times[c, d]$ ，令 $F$ 满足式 $\eqref{F的定义}$ 中的定义，则由Fubini定理可知，

$$\iint\limits_Df(x, y)dA = \iint\limits_RF(x, y)dA = \int_a^b\int_c^dF(x, y)dydx$$

观察到在 $(x, y)$ 在 $D$ 之外时 $F(x, y) = 0$ ，而在 $g_1(x)\le y\le g_2(x)$ 时 $F(x, y) = f(x, y)$ ，则

$$\int_c^dF(x, y)dy = \int_{g_1(x)}^{g_2(x)}F(x, y)dy = \int_{g_1(x)}^{g_2(x)}f(x, y)dy$$

因此我们有

总结

当 $f$ 在满足

$$D = \{(x, y)\ |\ a\le x\le b,\ g_1(x)\le y\le g_2(x)\}$$

的第一类积分区域 $D$ 内连续时，则

$$\iint\limits_Df(x, y)dA = \int_a^b\int_{g_1(x)}^{g_2(x)}f(x, y)dydx \tag{2.3}\label{第一类二重积分定义}.$$

第二类二重积分

类似地，当积分区域 $D$ 满足

$$D = \{(x, y)\ |\ c\le y\le d,\ h_1(y)\le x\le h_2(y)\}\\ (其中h_1和h_2在[c, d]内连续)$$

时， $f$ 满足

$$\iint\limits_Df(x, y)dA = \int_c^d\int_{h_1(y)}^{h_2(y)}f(x, y)dxdy \tag{2.4}\label{第二类二重积分定义}$$

其中 $D$ 为第二类积分区域。

二重积分的性质

• 性质1

  $$\iint\limits_D[f(x, y) + g(x, y)]dA = \iint\limits_Df(x, y)dA + \iint\limits_Dg(x, y)dA \tag{2.5}\label{性质1}$$

• 性质2

  $$\iint\limits_Dcf(x, y)dA = c\iint\limits_Df(x, y)dA \qquad (c为常量) \tag{2.6}\label{性质2}$$

• 性质3

  当所有在 $D$ 内的 $(x, y)$ 满足 $f(x, y)\ge g(x, y)$ 时，有

  $$\iint\limits_Df(x, y)dA \ge \iint\limits_Dg(x, y)dA \tag{2.7}\label{性质3}$$

• 性质4

  当 $D = D_1\bigcup D_2$ ，且 $D_1$ 和 $D_2$ 除了个别点之外没有重合范围时，

  $$\iint\limits_Df(x, y)dA = \iint\limits_{D_1}f(x, y)dA + \iint\limits_{D_2}f(x, y)dA \tag{2.8}\label{性质4}$$

  这个性质和一重积分的性质 $\int_a^bf(x)dx = \int_a^cf(x)dx + \int_c^bf(x)dx$ 很像。

• 性质5

  $$\iint\limits_D1dA = A(D) \tag{2.9}\label{性质5}$$

• 性质6

  如果所有在 $D$ 内的 $(x, y)$ 满足 $m\le f(x, y)\le M$ ，则

  $$mA(D)\le \iint\limits_Df(x, y)dA\le MA(D)\ \tag{2.10}\label{性质6}$$