Calculus笔记-15.1-矩形范围的二重积分

Calculus笔记-15.1-矩形范围的二重积分

定积分的回顾

• 一元定积分的定义：

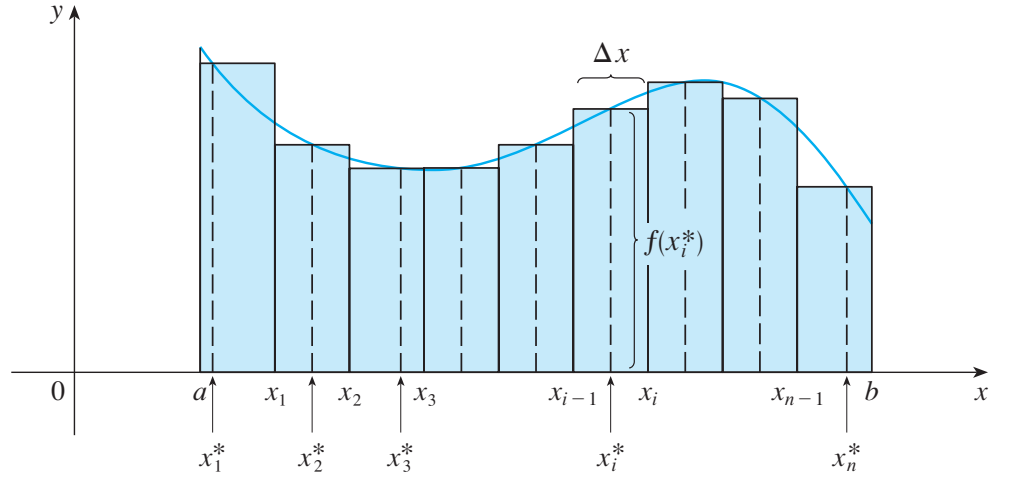
  如果 $f(x)$ 在 $a\le x\le b$ 有定义, 我们将范围 $[a, b]$ 分解成 $n$ 个子区间 $[x_{i - 1}, x_i]$ ，每个区间有定长 $\Delta x = (b - a) / n$ ，设这些子区间的采样点为 $x_i^*$ ， 则有黎曼和

  $$\sum_{i = 1}^n f(x_i^*)\Delta x$$

  令 $n\to\infty$ ，则我们有 $f$ 从 $a$ 变化到 $b$ 的定积分：

  $$\int_a^b f(x)dx = \lim_{n\to\infty}\sum_{i = 1}^nf(x_i^*)\Delta x$$

  当 $f(x)\ge 0$ 时，这个黎曼和表示用下图中近似矩形的面积之和，而 $\int_a^b f(x)dx$ 表示 $y = f(x)$ 从 $a$ 变化到 $b$ 时曲线下的面积。

  

体积和二重积分

设函数二元 $f$ 在闭矩形区域

$$R = [a, b]\times[c, d] = \{(x, y)\in\mathbb{R}^2|a\le x\le b, c\le y\le d\}$$

有定义，且 $f(x)\ge 0$ ，则 $f$ 的图像是 $z = f(x, y)$ 所定义的曲面。

令 $S$ 表示在 $R$ 和 $f$ 的图像之间的填充物，则

$$S = \{(x, y, z)\in\mathbb{R}^3|0\le z\le f(x, y), (x, y)\in\mathbb{R}\}$$

如何寻找 $S$ 的体积？

• 将矩形 $R$ 分解成子矩形

  • 将区间 $[a, b]$ 分解成 $m$ 个子矩形 $[x_{i - 1}, x_i]$ ，每个长 $\Delta x = (b - a) / m$

  • 将区间 $[c, d]$ 分解成 $n$ 个子矩形 $[y_{i - 1}, y_i]$ ，每个长 $\Delta y = (d - c) / n$

    则我们有：

    $$R_{ij} = [x_{i - 1}, x_i]\times[y_{j - 1}, y_j] = \{(x, y)|x_{i - 1}\le x\le x_i, y_{j - 1}\le y\le y_j\}$$

    每个面积为 $\Delta A = \Delta x\Delta y$ .

• 通过采样来进行估计

  在每一个 $R_{ij}$ 内采样点 $(x_{ij}^*, y_{ij}^*)$ ，则我们可以用底为 $R_{ij}$ ，高为 $f(x_{ij}^*, y_{ij}^*)$ 的窄长方体来估计 $S$ 的一部分，其体积为

  $$f(x_{ij}^*, y_{ij}^*)\Delta A$$

  重复这样的过程，我们可以得到对 $S$ 体积的一个估计：

  $$V\approx \sum_{i = 1}^m\sum_{j = 1}^nf(x_{ij}^*, y_{ij}^*)\Delta A$$

  直觉告诉我们，当 $m$ 和 $n$ 越来越大时，这个估计会变得更准确，则有：

  $$V\approx\lim_{m, n\to\infty}\sum_{i = 1}^m\sum_{j = 1}^nf(x_{ij}^*, y_{ij}^*)\Delta A\tag{1.1}\label{二重黎曼和估计}$$

  我们用式 $\eqref{二重黎曼和估计}$ 来定义 $S$ 的体积。

定义

• $f$ 对矩形面积 $R$ 的二重积分为

  $$\iint\limits_Rf(x, y)dA = \lim_{m, n\to\infty}\sum_{i = 1}^m\sum_{j = 1}^nf(x_{ij}^*, y_{ij}^*)\Delta A\tag{1.2}\label{二重积分定义}$$

• 更准确的定义：

  对于任意 $\epsilon > 0$ ，存在整数 $N$ 使得

  $$\left|\iint\limits_Rf(x, y)dA - \sum_{i = 1}^m\sum_{j = 1}^nf(x_{ij}^*, y_{ij}^*)\Delta A\right| < \epsilon$$

  对于任意大于 $N$ 的整数 $m$ , $n$ ， $R$ 内的采样点 $(x_{ij}^*, y_{ij}^*)$ 成立。

• 更简洁的定义

  当定义 $\eqref{二重积分定义}$ 的极限存在时，我们称 $f$ （在区间 $R$ 内）可积分。连续函数总是可积分。事实上，只要 $f$ 在区间 $R$ 内只有有限个不连续点，它总是可积分的。

  采样点 $(x_{ij}^*, y_{ij}^*)$ 可以取子区间 $R_{ij}$ 内的任意点，如果我们取区间的右端点，二重积分的定义会显得比较简洁：

  $$\iint\limits_Rf(x, y)dA = \lim_{m, n\to\infty}\sum_{i = 1}^m\sum_{j = 1}^nf(x_i, y_j)\Delta A$$

• 体积的表示

  通过比较 $\eqref{二重黎曼和估计}$ 和 $\eqref{二重积分定义}$ ，我们知道体积可以写作二重积分的形式：

  如果 $f(x, y)\ge 0$ ，则矩形 $R$ 和曲面 $z = f(x, y)$ 之间的体积为：

  $$V = \iint\limits_Rf(x, y)dA$$

  $\eqref{二重黎曼和估计}$ 中的和

  $$\sum_{i = 1}^m\sum_{j = 1}^nf(x_{ij}^*, y_{ij}^*)\Delta A$$

  又被称作二重黎曼和。

二重积分的积分中值定理

$$\iint\limits_Rf(x, y)dA\approx\sum_{i = 1}^m\sum_{j = 1}^nf(\bar{x}_i, \bar{y}_j)\Delta A$$

其中 $\bar{x}_i$ 和 $\bar{y}_j$ 分别是子区间 $[x_{i - 1}, x_i]$ 和 $[y_{j - 1}, y_j]$ 的中值。

Fubini定理

当 $f$ 在矩形区间 $R = \{(x, y)|a\le x\le b, c\le y\le d\}$ 内连续时，

$$\iint\limits_Rf(x, y)dA = \int_a^b\int_c^df(x, y)dydx = \int_c^d\int_a^bf(x, y)dxdy$$

更广泛地，这个定理在 $f$ 只在区间 $R$ 的有限个点上不连续时也成立。

乘法定理

$$\iint\limits_Rg(x)h(y)dA = \int_a^bg(x)dx\int_c^dh(y)dy\qquad \text{其中} R = [a, b]\times[c, d]$$

平均值

• 二元函数 $f$ 在矩形区间内的平均值为

  $$f_\text{ave} = \frac1{A(R)}\iint\limits_Rf(x, y)dA$$

  其中 $A(R)$ 为 $R$ 的面积。

• 当 $f(x, y)\ge 0$ 时，式

  $$f_\text{ave}A(R) = \iint\limits_Rf(x, y)dA$$

  说明底为 $R$ ，高为 $f_\text{ave}$ 的矩形的体积和 $f$ 所围成的物体体积相同。