GAMES101笔记：Lecture04-变换_续

2024-05-03

GAMES101笔记：Lecture04 变换_续

二维情况的旋转变换

$\mathbf{R}_\theta = \begin{pmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix}$ $\mathbf{R}_{-\theta} = \begin{pmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix} = \mathbf{R}_\theta^T$ $\mathbf{R}_{-\theta} = \mathbf{R}_\theta^{-1}\text{(by definition)}$

当一个矩阵的逆等于其转置时，这个矩阵被称为正交矩阵

Syllabus

Viewing transformation
- View/Camera transformation
- Projection transformation
  - Orthographic projection
  - Perspective projection

三维变换(3D transformations)

Scale

$\mathbf{S}(s_x, s_y, s_z) = \begin{pmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}$

Translation

$\mathbf{T}(s_x, s_y, s_z) = \begin{pmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}$

Rotation

绕单轴旋转：

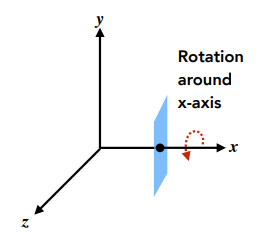
$\mathbf{R}_x(\alpha) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha & 0 \\ 0 & \sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}$ $\mathbf{R}_y(\alpha) = \begin{pmatrix} \cos\alpha & 0 & \sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\alpha & 0 & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}$ $\mathbf{R}_z(\alpha) = \begin{pmatrix} \cos\alpha & -\sin\alpha & 0 & 0 \\ \sin\alpha & \cos\alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}$

绕任意轴的旋转

分别绕 $x, y, z$ 轴旋转指定角度p

$\mathbf{R}_{xyz}(\alpha, \beta, \gamma) = \mathbf{R}_x(\alpha) \mathbf{R}_y(\beta) \mathbf{R}_z(\gamma)$

So-called Euler angles（欧拉角）
Often used in flight simulators: roll, pitch, yaw（如下图）

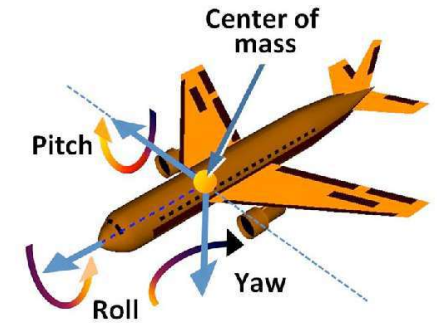
绕指定（过原点的）轴旋转指定角度

Rotation by angle $\alpha$ around axis $\mathbf{n}$ （罗德里德斯公式）

$\mathbf{R}(\mathbf{n}, \alpha) = \cos(\alpha)\mathbf{I} + (1 - \cos(\alpha))\mathbf{n}\mathbf{n}^T + \sin(\alpha) \underbrace{\begin{pmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \\ \end{pmatrix}}_\mathbf{N}$

如何绕非过原点的轴旋转？

先将旋转轴移到原点，执行旋转，再平移回去

四元数

主要用于旋转插值

观测变换(Viewing transformation)

什么是观测变换？
思考照一张相的过程
- 寻找一个好的地方（模型变换(model transformation)）
- 寻找一个好的角度（视图变换(view transformation)）
- 拍照（投影变换(projection transformation)
  
  简称MVP变换
  
  （最后还有一个将正则化的正方体拉伸成屏幕画面大小的变换，被称为视口变换(Viewport transformation)

视图变换(View / Camera Transformation)

如何进行视图变换？

首先定义相机
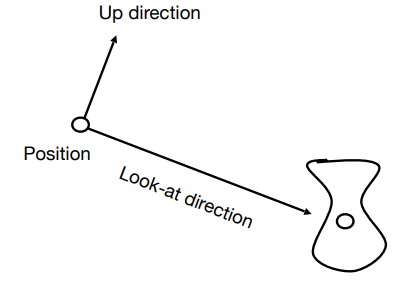
- 位置 $\vec{e}$
- 观测方向 $\vec{g}$
- 向上方向 $\hat{t}$
  
  （假设与观测方向垂直）
关键的观察
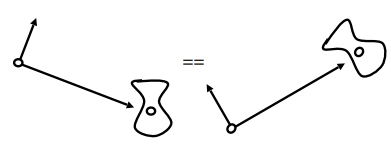
- 如果相机和被观测物体同时运动时，这张”照片“会是一样的
可以将相机的位置变换为：
- 固定在原点，向上方向为Y轴，向着-Z方向观察
- 然后将物体与相机一同变换
使用 $M_{view}$ 对相机施加变换
- 如此将相机摆放在原点，向上方向为Y轴，向-Z方向观察
$M_{view}$ 的数学描述
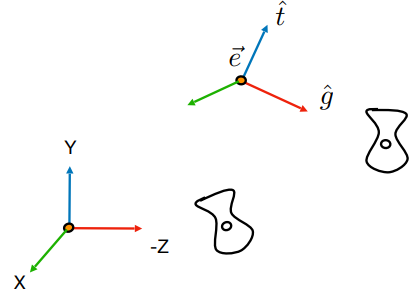
- 将 $e$ 平移到原点
- 将 $g$ 旋转到 $-Z$ 方向
- 将 $t$ 旋转到 $Y$ 方向
- 将 $(g\times t)$ 旋转到 $X$ 方向
  
  （并不好写出来）
- 定义 $M_{view} = R_{view}T_{view}$
- 将 $e$ 平移到原点
  $T_{view} = \begin{bmatrix} 1&0&0&-x_e\\0&1&0&-y_e\\0&0&1&-z_e\\0&0&0&1 \end{bmatrix}$
- 将 $g$ 旋转到 $-Z$ , 将 $t$ 旋转到 $Y$ , 将 $(g\times t)$ 旋转到 $X$
- 考虑它的逆变换：将 $X$ 旋转到 $(g\times t)$ , 将 $Y$ 旋转到 $t$ , 将 $Z$ 旋转到 $-g$
  
  由于旋转矩阵是正交矩阵，所以
  $R_{view}^{-1} = R_{view}^T$
  代入
  $R_{view}^{-1} =\begin{bmatrix} x_{\hat{g}\times\hat{t}}&x_{t}&x_{-g}&0\\ y_{\hat{g}\times\hat{t}}&y_{t}&y_{-g}&0\\ z_{\hat{g}\times\hat{t}}&z_{t}&z_{-g}&0\\ 0&0&0&1 \end{bmatrix}$
  得
  $R_{view} =\begin{bmatrix} x_{\hat{g}\times\hat{t}}& y_{\hat{g}\times\hat{t}}& z_{\hat{g}\times\hat{t}}& 0\\ x_{t}&y_{t}&z_{t}&0\\ x_{-g}&y_{-g}&z_{-g}&0\\ 0&0&0&1 \end{bmatrix}.$
总结
- 将物体与摄像机一同变换
- 目标：将相机固定在原点，向上方向为Y轴，向着-Z方向观察
- 公式： $M_{view} = R_{view}T_{view} = \begin{bmatrix} x_{\hat{g}\times\hat{t}}& y_{\hat{g}\times\hat{t}}& z_{\hat{g}\times\hat{t}}& 0\\ x_{t}&y_{t}&z_{t}&0\\ x_{-g}&y_{-g}&z_{-g}&0\\ 0&0&0&1 \end{bmatrix} \begin{bmatrix} 1&0&0&-x_e\\0&1&0&-y_e\\0&0&1&-z_e\\0&0&0&1 \end{bmatrix}$

投影变换(Projection transformation)

Projection in Computer Graphics
- 3D to 2D
- Orthographic projection
- Perspective projection
正交投影与透视投影的区别
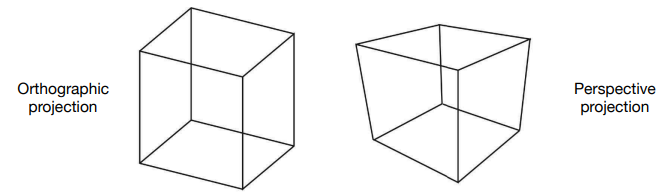
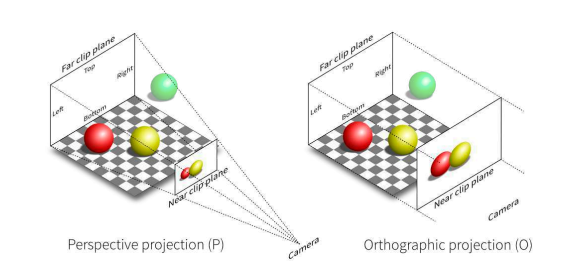
- 正交投影变换后的图片满足严格平行，但不符合人眼的观察原理
- 透视投影变换后的平行线会汇聚于一点，会有“近大远小”的现象

正交投影(Orthographic projection)

假设摄像机位于无限远的距离

一种简单的理解方法

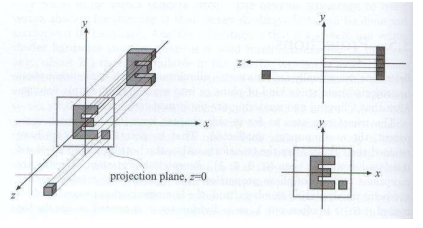
将相机固定在原点，向上方向为Y轴，向着-Z方向观察
将 $Z$ 轴坐标“丢掉”
然后将结果矩形平移并缩放到 $\begin{bmatrix}-1, 1\end{bmatrix}^2$

正规做法

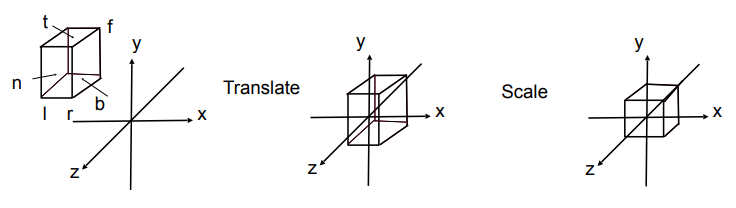
将空间范围 $[l, r]\times[b, t]\times[f, n]$ 映射到”正则(canonical)”正方体 $[-1, 1] ^ 3$ 上

步骤：

将长方体(cuboid)的重心平移到原点
缩放到“正则”正方体大小

注意（一个不直观的定义）：

将 $-Z$ 方向定义为“远”， $Z$ 方向定义为“近”
因为摄像机是朝向 $-Z$ 方向“看”的

变换矩阵(Transformation matrix)

先将重心平移(translate)到原点，再将长/宽/高缩放为2
$\begin{align} M_{ortho} &= \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & 0 \\ 0 & \frac{2}{t - b} & 0 & 0 \\ 0 & 0 & \frac{2}{n - f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r + l}{2} \\ 0 & 1 & 0 & -\frac{t + b}{2} \\ 0 & 0 & 1 & -\frac{n + f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix}\\ &= \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & \frac{r + l}{l - r} \\ 0 & \frac{2}{t - b} & 0 & \frac{t + b}{b - t} \\ 0 & 0 & \frac{2}{n - f} & \frac{n + f}{f - n} \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{align}$
注意：

$z$ 长度上缩放系数的分母是 $n - f$ , 因为 $n$ 的 $z$ 坐标大于 $f$ 的 $z$ 坐标

透视投影(Perspective projection)

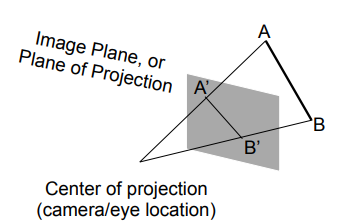
如上图，假设摄像机位于有限远的一点上，可视范围被称为视锥体(frustum)，视锥体的一端为渲染范围的最远处，一端为投影平面(Plane of Projection)

利用到的齐次坐标性质：

$(x, y, z, 1)$ , $(kx, ky, kz, k)(k \neq 0)$ , $(xz, yz, z^2, z)(z \neq 0)$ 都表示在三维空间中的点 $(x, y, z)$
如何进行透视投影：
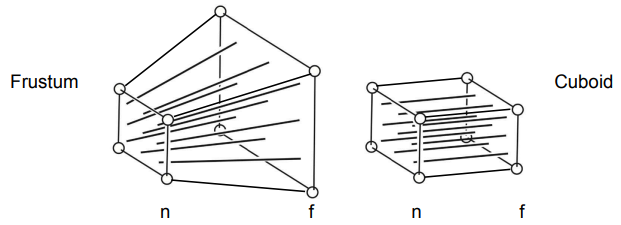
- 首先将视锥体”压缩”成一个长方体 $(n\to n),\ f\to f)\ (M_{persp\to ortho})$
- 再进行一次正交投影 ( $M_{ortho}$ )
几个规定：
- 近平面永远不变
- 对于远平面上的点，只有 $x,\ y$ 发生变化，而 $z$ 不变
- （位于中间的平面 $z$ 坐标可能会发生改变）
- 远平面的中心点坐标不变
如何寻找变换：
- 寻找变换后的点 $(x^\prime, y^\prime, z^\prime)$ 与原始点 $(x, y, z)$ 的关系
- 观察侧视图：
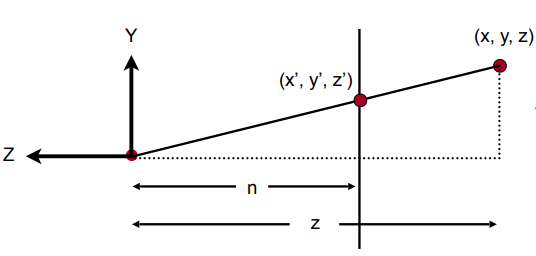
- 由图中的相似三角形可以得出：
  $y^\prime = \frac{n}{z}y$
  同理：
  $x^\prime = \frac{n}{z}x$
用齐次坐标表示：
$\begin{pmatrix}x\\y\\z\\1\end{pmatrix} \Rightarrow \begin{pmatrix} \frac{nx}z\\\frac{ny}z\\\text{unknown}\\1 \end{pmatrix} == \begin{pmatrix} nx\\ny\\\text{still unknown}\\z \end{pmatrix}$
因此可以将 $M_{persp\to ortho}$ 的部分位置填写上
$M_{persp\to ortho} = \begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ ? & ? & ? & ?\\ 0 & 0 & 1 & 0 \end{pmatrix}$
观察：第三行和 $z$ 有关
- 任何近平面上的点的坐标不会变化
- 任何远平面上的点的 $z$ 坐标不会变化
任何近平面上的点的坐标不会变化
$\begin{pmatrix}x\\y\\n\\1\end{pmatrix} \Rightarrow \begin{pmatrix}x\\y\\n\\1\end{pmatrix} == \begin{pmatrix}nx\\ny\\n^2\\n\end{pmatrix}$
所以第三行一定是 $\begin{pmatrix}0&0&A&B\end{pmatrix}$ 的形式，因为：
$\begin{pmatrix}0&0&A&B\end{pmatrix} \begin{pmatrix}x\\y\\n\\1\end{pmatrix}=n^2 \quad (n^2\text{和x, y无关})$ $\begin{pmatrix}0&0&A&B\end{pmatrix} \begin{pmatrix}x\\y\\n\\1\end{pmatrix}=n^2 \Rightarrow An + B = n^2$

任何远平面上的点的 $z$ 坐标不会变化：
$\begin{pmatrix}0\\0\\f\\1\end{pmatrix} \Rightarrow \begin{pmatrix}0\\0\\f\\1\end{pmatrix} == \begin{pmatrix}0\\0\\f^2\\f\end{pmatrix} \Rightarrow Af + B = f^2$
联立上式解出 A 和 B ：
$\begin{aligned} An + B &= n^2\\ Af + B &= f^2 \end{aligned} \implies \begin{aligned} A &= n + f\\ B &= -nf \end{aligned}$
因此 $M_{persp\to ortho}$ 的每一项都得知了

总结

$\begin{align} M_{persp} &= M_{ortho}M_{persp\to ortho}\\ &= \begin{pmatrix} \frac{2}{r - l} & 0 & 0 & \frac{r + l}{l - r} \\ 0 & \frac{2}{t - b} & 0 & \frac{t + b}{b - t} \\ 0 & 0 & \frac{2}{n - f} & \frac{n + f}{f - n} \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & 1 & 0 \end{pmatrix}\\ &= \begin{pmatrix} \frac{2n}{r - l} & 0 & \frac{r + l}{l - r} & 0 \\ 0 & \frac{2n}{t - b} & \frac{t + b}{b - t} & 0 \\ 0 & 0 & \frac{n + f}{n - f} & \frac{2nf}{f - n} \\ 0 & 0 & 1 & 0 \end{pmatrix}. \end{align}$

视口变换(Viewport transformation)(注1)

将空间 $[-1, 1]^2$ 变换到 $[0, width]\times[0, height]$ ，和正交变换的原理相同，只不过反过来，先缩放再平移：

$M_{viewport} = \begin{pmatrix} \frac{width}2 & 0 & 0 & \frac{width}2 \\ 0 & \frac{height}2 & 0 & \frac{height}2 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$

总结

$M = M_{viewport}M_{persp}M_{view}M_{model}.$

注1：此部分可参考下文

计算机图形学二：视图变换(坐标系转化，正交投影，透视投影，视口变换)_正交变换投影变换-CSDN博客