GAMES101笔记:Lecture03 变换
Syllabus
- Transformation
- Today
- Why study transformation
- 2D transformations: rotation, scale, shear
- Homogeneous coordinates
- Composing transforms
- 3D transformations
为什么要学习变换
变换的两大分类
- 模型变换(Modeling)
- 视图变换(Viewing)
具体的变换类型
位移变换(translation)

旋转变换(rotation)

缩放变换(scaling)

视图:(3D到2D的)投影(projection)
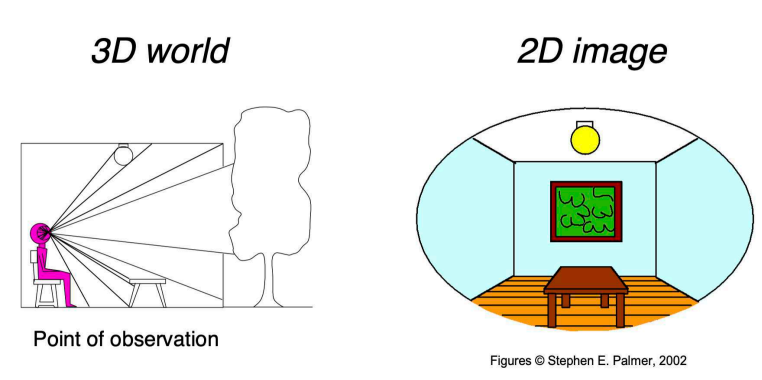
二维变换(2D transformations)
缩放变换(scaling)
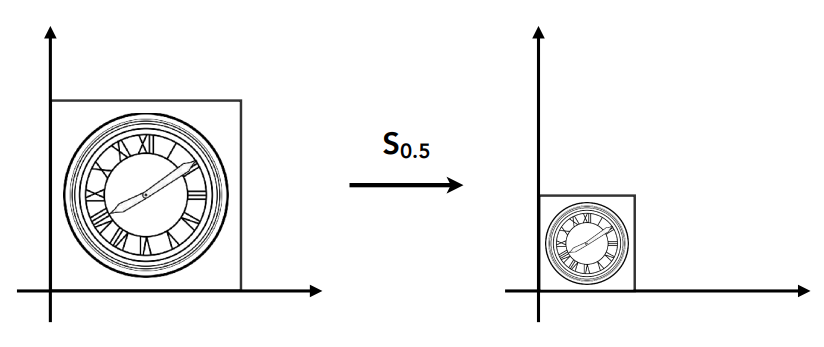
数学形式
矩阵形式
非均匀缩放
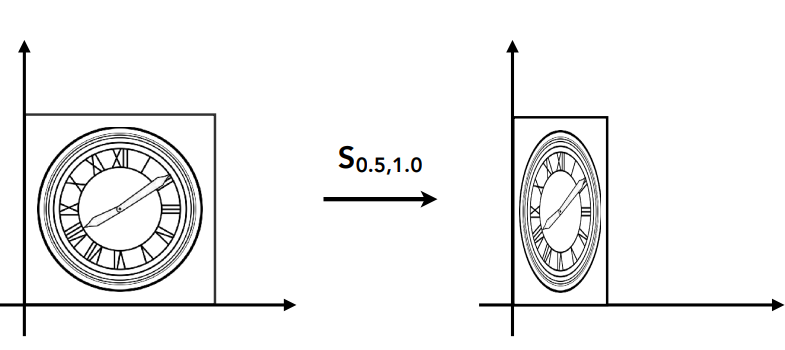
反射变换(Reflection):水平反射
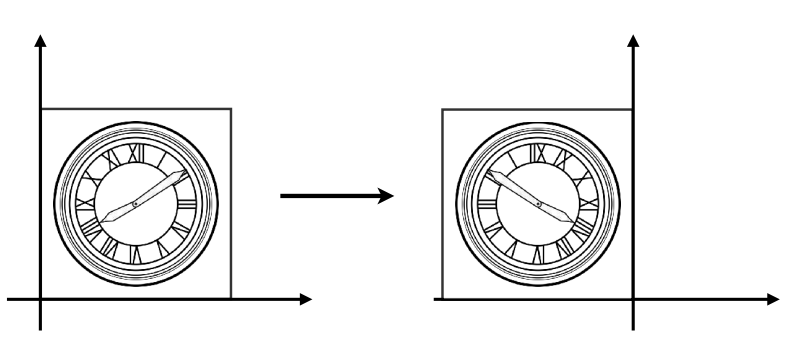
代数形式
矩阵形式
切变(Shearing)
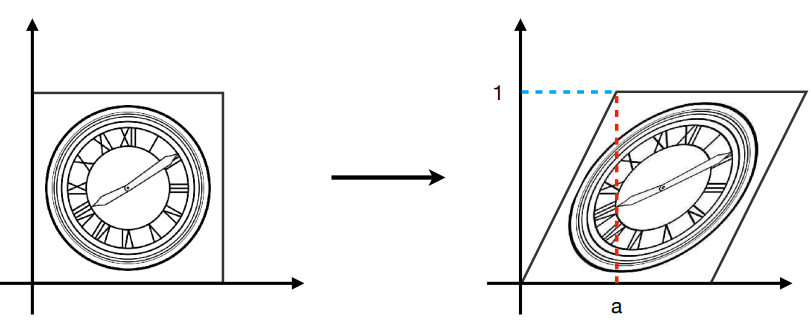
矩阵形式
旋转
在平面内默认关于原点,默认方向为逆时针方向的旋转:
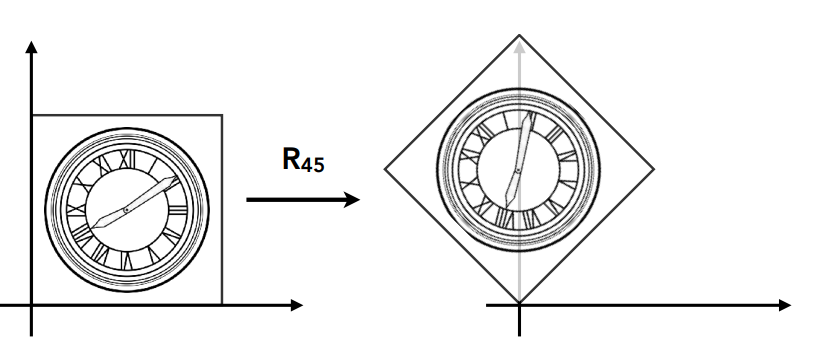
旋转矩阵
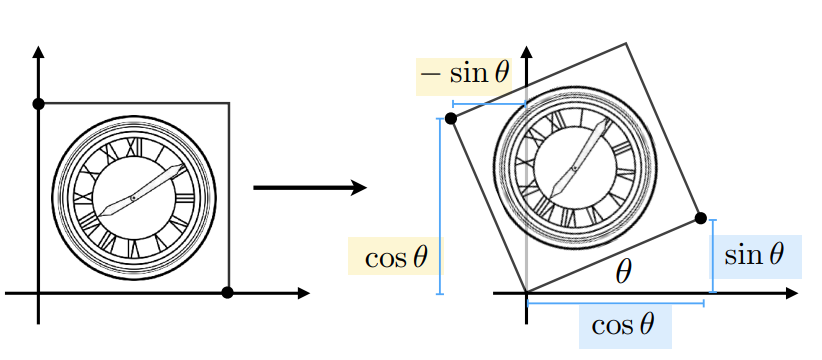
代入坐标轴变换的推导
设:
则:
所以
即
公理化证明
设旋转前 $x$ , $y$ 分别为 $x_0$ , $y_0$ ,选择后 $x$ , $y$ 分别为 $x_1$ , $y_1$ ,则:
代入
得:
线性组合的通式
线性变换能够由一个(同一维度的)矩阵表示
齐次坐标(Homogenous coordinate)
引入
平移变换(Translation)
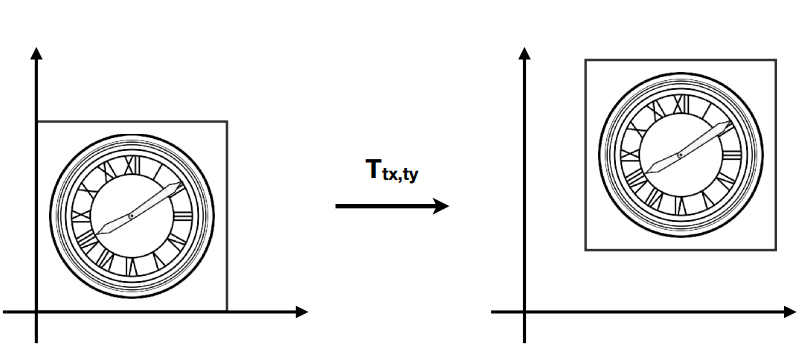
数学描述
问题:
平移变换不能用矩阵形式表示
我们并不想将平移作为特例来处理
是否有一个统一且代价合理的方法来统一所有变换?
- 考虑trade off
解决方法:齐次坐标
齐次坐标的表示
为二维坐标增加一个维度(w坐标)
- 2D point = $(x, y, 1)^T$
- 2D vector = $(x, y, 0)^T$
变换的矩阵表示
为何将向量和点区别对待?
因为向量具有平移不变性
w坐标的意义
- vector + vecor = vecor
- point - point = vecor
- point + vector = point
- point + point = ??
在齐次坐标中,
仿射变换(Affine Transformations)
Affine map = linear map + translation
Using homogenous coordinates:
2D Transformations
Scale
Rotation
Translation
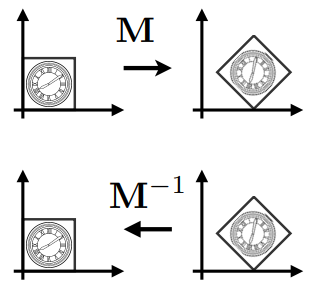
逆变换(Inverse tranform)
$\mathbf{M}^{-1}$ 是变换 $\mathbf{M}$ 在矩阵和几何意义上的逆操作
变换的组合(Composing translation)
顺序:
先旋转再平移
矩阵运算顺序:
从右到左
Composing Transforms
Sequence of affine transforms $\mathbf{A_1}, \mathbf{A_2}, \mathbf{A_3}, \dots$
Compose by matrix multiplication
- Very important for performance!
变换的分解(Decomposing Complex Transforms)
以任意一个点为中心进行旋转
- 将中心平移到原点
- 旋转
- 再平移回去
矩阵表示
三维变换(3D Transforms)
使用齐次坐标表示
- 3D point = $(x, y, z, 1)^T$
- 3D vector= $(x, y, z, 0)^T$
一般来说,$(x, y, z, w)(w\neq0)$ 表示三维空间中的点
使用4x4矩阵来表示仿射变换
问题
应该以什么顺序执行?先表示平移还是先表示线性变换?
答案
先线性变换再平移
