GAMES101笔记：Lecture02-线性代数复习

2024-05-02

GAMES101笔记：Lecture02 线性代数复习

图形学的依赖知识

数学知识
- 线性代数、微积分、统计
物理
- 光学、力学
杂项
- 信号处理
- 数值分析
一些美感

本课程内容

更依赖于线性代数
- 向量（点乘、叉乘······）
- 矩阵（矩阵-矩阵、矩阵-向量······）

示例

蜗牛的旋转：

插值
粒子光效

向量

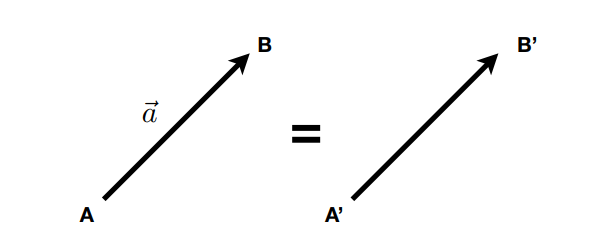
通常写为 $\vec{a}$ 或 $\boldsymbol{a}$
或用起点/终点 $\overrightarrow{AB} = B - A$
具有方向与长度
没有绝对的起点

向量正则化

向量的长度（模）写作 $|{\vec{a}}|$
单位向量
- 长度为 $1$ 的向量
- 寻找给定向量的单位向量（正则化）： $\hat{a} = \vec{a}/|\vec{a}|$
- 用于表示方向

向量求和

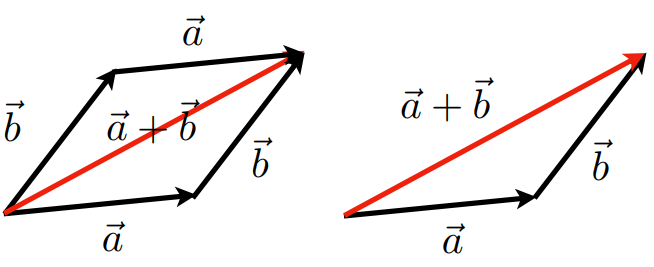
几何上：平行四边形法则和三角形法则
代数上：直接将坐标相加

笛卡尔坐标系

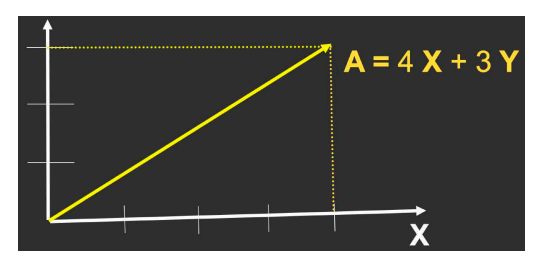
X和Y可以是任何（一般是正交单位）向量

$\mathbf{A} = \begin{pmatrix}x\\y\end{pmatrix} \qquad\mathbf{A}^T = \begin{pmatrix}x, y\end{pmatrix} \qquad\|\mathbf{A}\| = \sqrt{x^2 + y^2}$

在图形学上，默认处理列向量
定义直角坐标的意义：
- 方便计算向量长度

向量乘法

点乘
叉乘
正交基和坐标系(Orthonormal bases and coordinate frames)

点（数）乘

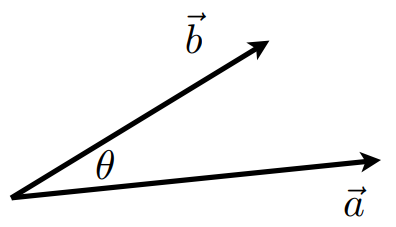
$\vec{a}\cdot\vec{b} = \|\vec{a}\|\|\vec{b}\|\cos{\theta}$ $\cos{\theta} = \frac{\vec{a}\cdot\vec{b}}{\|\vec{a}\|\|\vec{b}\|}$

对于单位向量：
$\cos{\theta} = \hat{a}\cdot\hat{b}$
向量的点乘是一个数
运算法则（性质）

$\vec{a}\cdot\vec{b} = \vec{b}\cdot\vec{a}\text{（交换律）}$ $\vec{a}\cdot(\vec{b} + \vec{c}) = \vec{a}\cdot\vec{b} + \vec{a}\cdot\vec{c}\text{（分配律）}$ $(k\vec{a})\cdot\vec{b} = \vec{a}\cdot(k\vec{b}) = k(\vec{a}\cdot\vec{b})\text{（结合律）}$

笛卡尔坐标系中的点乘

按元素（Component-wise）分别做乘法再相加
- 在二维空间中：
  $\vec{a}\cdot\vec{b} = \begin{pmatrix}x_a\\y_a\end{pmatrix}\cdot \begin{pmatrix}x_b\\y_b\end{pmatrix} = x_ax_b + y_ay_b$
- 在三维空间中：
  $\vec{a}\cdot\vec{b} = \begin{pmatrix}x_a\\y_a\\z_a\end{pmatrix}\cdot \begin{pmatrix}x_b\\y_b\\z_b\end{pmatrix} = x_ax_b + y_ay_b + z_az_b$

图形学中的点乘

寻找两个向量的夹角

（比如光源和照射表面的夹角余弦）
寻找一个向量在另一个向量上的投影

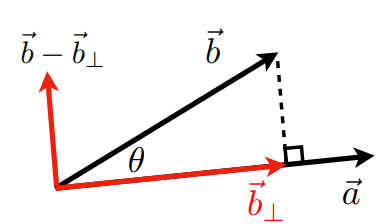
投影与点乘

$\vec{b}_\perp$： $\vec{b}$ 在 $\vec{a}$ 上的投影
- $\vec{b}_\perp$ 一定沿着 $\vec{a}$ （或 $\hat{a}$ ）的方向
  - $\vec{b}_\perp = k\hat{a}$
- 模长k是多少？
  - $k = |\vec{b}_\perp| = |\vec{b}|\cos{\theta}$

寻找投影的好处

测量两个方向有多接近
分解向量（上图）
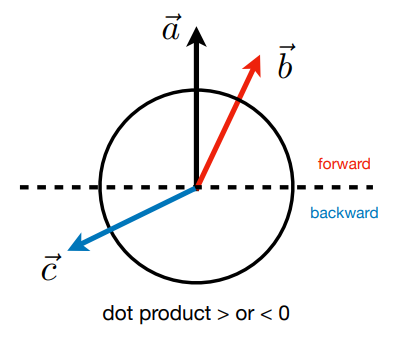
确定向前/向后（下图）：
- 根据点乘的正负性判断

向量的叉乘

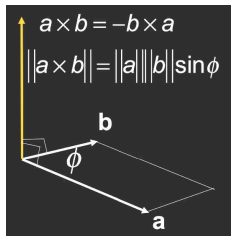
叉乘的结果与两个输入向量垂直
由右手法则确定方向
在建立坐标系时很有用

向量叉乘的性质

$\begin{align} \vec{x}\times\vec{y} = +\vec{z}\\ \vec{y}\times\vec{x} = -\vec{z}\\ \vec{y}\times\vec{z} = +\vec{x}\\ \vec{z}\times\vec{y} = -\vec{x}\\ \vec{z}\times\vec{x} = +\vec{y}\\ \vec{x}\times\vec{z} = -\vec{y}\\ \\ \vec{a}\times\vec{b} = -\vec{b}\times\vec{a}\\ \vec{a}\times\vec{a} = \vec{0}\\ \vec{a}\times(\vec{b} + \vec{c}) = \vec{a}\times\vec{b} + \vec{a}\times\vec{c}\\ \vec{a}\times(k\vec{b}) = k(\vec{a}\times\vec{b}) \end{align}$

向量叉乘的坐标系法则

$\vec{a}\times\vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ x_a & y_a & z_a \\ x_b & y_b & z_b \end{vmatrix}$

叉乘在图形学中的应用

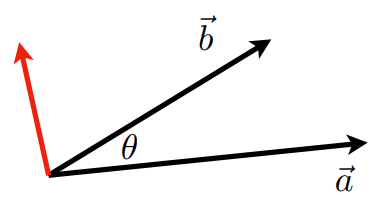
判定左/右

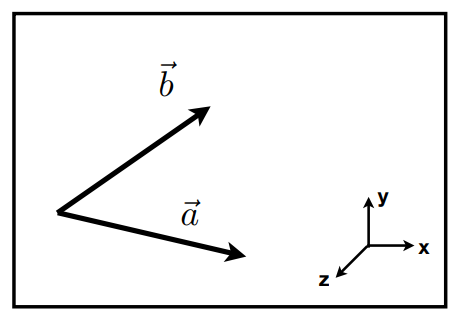
如上图，当$\vec{a}\times\vec{b}$ 朝向正方向时，说明 $\vec{b}$ 在 $\vec{a}$ 的左侧
判定内/外

当

朝向同侧时，P点在三角形ABC内部
- 三角形的绕序不影响结果
- 当叉乘同为零向量时怎么判断：
  - Corner Case（自己决定）

正交基/坐标系

在表示点、位置和方位时很重要
常用的坐标系
- Global, local, world, model, parts of model···
重要问题：在坐标系/空间基之间的转换

正交基的定义

任何三个三维向量的集满足：
$\|\vec{u}\| = \|\vec{v}\| = \|\vec{w}\| = 1$ $\vec{u}\cdot\vec{v} = \vec{v}\cdot\vec{w} = \vec{u}\cdot\vec{w} = 0$ $\vec{w} = \vec{u}\times\vec{v}\text{（右手系）}$ $\vec{p} = \underbrace{(\vec{p}\cdot\vec{u})}_\text{(投影长度)}\vec{u} + (\vec{p}\cdot\vec{v})\vec{v} + (\vec{p}\cdot\vec{w})\vec{w}$

矩阵

二维数组
在图形学中被广泛(pervasively)用于表示变换
- 移动、旋转、缩放、错切······

什么是矩阵

数字构成的数组(m x n = m行n列)
加法与数乘只需要按元素进行

矩阵-矩阵乘积

要求：$A\times B$ 要求 $A$ 的列数= $B$ 的行数

$(M\times N)(N\times P) = (M\times P)$
结果矩阵中的每一个元素 $(i, j)$ 等于 $A$ 矩阵的第 $i$ 行与 $B$ 矩阵的第 $j$ 列的点乘
性质
- 不满足交换律
  
  (AB和BA一般不同)
- 满足结合律和分配律

矩阵-向量乘积

假定向量是列向量(m x 1)
空间点变换的关键

矩阵转置

将行和列互换
性质
$(AB)^T = B^TA^T$

单位矩阵和矩阵的逆

$I_{n\times n} = \begin{pmatrix} 1 & 0 & \cdots & 0\\ 0 & 0 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & 1 \end{pmatrix}_{n\times n}$ $AA^{-1} = A^{-1}A = I$ $(AB)^{-1} = B^{-1}A^{-1}$

矩阵形式的向量乘法

点乘
$\begin{align} \vec{a}\cdot\vec{b} &=& \vec{a}^T\vec{b}\notag\\ &=& \begin{pmatrix}x_a & y_a & z_a\end{pmatrix} \begin{pmatrix}x_a \\ y_a \\ z_a\end{pmatrix}\notag\\ &=&(x_ax_b + y_ay_b + z_az_b) \end{align}$
叉乘
$\vec{a}\times\vec{b} = A^*b = \underbrace{\begin{pmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \end{pmatrix}}_\text{向量a的伴随矩阵(dual matrix)} \begin{pmatrix}x_b \\ y_b \\ z_b\end{pmatrix}$